
My role
Data Analysis & Research
Performing a comprehensive Multivariate Analysis, building a Linear Regression Model

Timeline
Jun ’23
Case study, openHPI
Data Science Bootcamp

Tools
Python
Jupyter
Office Suite
OVERVIEW
The Data
The Toyota Corolla Dataset was collected in 2004 to record the features and the prices of the second hand cars.
The Goal
Predict the price of a used car, and find which variables get more important when a car gets older.
Tools
Pandas and Numpy for basics,
Seaborn for analysis and visualization,
Matplotlib for visualization and correlation matrix,
Sklearn for linear model.
Methods
Statistics
Data Cleaning
Multivariate Analysis
Problem Statements
Data Visualization
Linear Regression
Research data *
I do not own the Corolla dataset, and I spent vast amount of time to find the source of it. Below you will find more information on this.
If you’d like to read this analysis in Kaggle, feel free to visit my page there.
* I performed this analysis only for educational purposes and to demonstrate my skills and how I approach to a dataset, that has a wide-range of variables, here in my online portfolio.
1 Introduction
Toyota Corolla dataset was given us as a practice set during the openHPI‘s Data Science Bootcamp 2023. It was introduced under the ‘EDA and Statistical Analysis’ section to demonstrate MVA studies. It was not an assignment but part of the lecture. Yet I wanted to play around and use the dataset to answer some other questions and then shared my analysis in the forum with the title ‘Getting charmingly lost in the Corolla dataset‘.
The instructors provided me useful feedback but some questions were still not answered (you’ll find them below). So I decided to dive deeper to hopefully find some explanations and (even if not) to gain further knowledge and skills on data analysis processes.
It’s better to underline that I am at the entry level in data science and I am aware of other methods and models that may fit better here. But I limited myself within MVA and Linear Regression.
I hope this work of mine will demonstrate how I approach to a dataset that has a wide-range of variables and what kind of reasonings I developed to some certain data analysis issues.
1.1 The Origin of the Dataset
Although there are a bunch of studies regarding this exact Corolla dataset on the web, it is not possible to find the initial source of it, at least publicly. I spent hours trying to find out where this dataset comes from, by whom it was collected and where it was shared. I did so, because I believe every data-related research should start with questioning the data itself. Besides, the unanswered questions in my initial analysis that I mentioned above might be a result of a dummy set, as the instructors were not able to clarify the source of it.
Unfortunately I did not find the main source but I guess I found where this set first appeared. If you want to read more about this research of mine, you can visit my post here.
1.2 What is this Dataset about?
I’ll stick with the only description that is available online:
“The file ToyotaCorolla.xls contains data on used cars (Toyota Corolla) on sale during late summer of 2004 in The Netherlands. It has 1436 records containing details on 38 attributes, including Price, Age, Kilometers, HP, and other specifications. The goal is to predict the price of a used Toyota Corolla based on its specifications.“
In the DS Bootcamp we were using this dataset for the same purpose. We were giving a set of values and were trying to predict the price. As I mentioned above, afterwards I came up with different questions just to practice the methods that were shown to us.
Let’s have a quick look at those attributes:
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as pltdf = pd.read_csv('/kaggle/input/toyotacorolladataset/ToyotaCorolla.csv')df.info()<class 'pandas.core.frame.DataFrame'> RangeIndex: 1436 entries, 0 to 1435 Data columns (total 39 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 Id 1436 non-null int64 1 Model 1436 non-null object 2 Price 1436 non-null int64 3 Age_08_04 1436 non-null int64 4 Mfg_Month 1436 non-null int64 5 Mfg_Year 1436 non-null int64 6 KM 1436 non-null int64 7 Fuel_Type 1436 non-null object 8 HP 1436 non-null int64 9 Met_Color 1436 non-null int64 10 Color 1436 non-null object 11 Automatic 1436 non-null int64 12 CC 1436 non-null int64 13 Doors 1436 non-null int64 14 Cylinders 1436 non-null int64 15 Gears 1436 non-null int64 16 Quarterly_Tax 1436 non-null int64 17 Weight 1436 non-null int64 18 Mfr_Guarantee 1436 non-null int64 19 BOVAG_Guarantee 1436 non-null int64 20 Guarantee_Period 1436 non-null int64 21 ABS 1436 non-null int64 22 Airbag_1 1436 non-null int64 23 Airbag_2 1436 non-null int64 24 Airco 1436 non-null int64 25 Automatic_airco 1436 non-null int64 26 Boardcomputer 1436 non-null int64 27 CD_Player 1436 non-null int64 28 Central_Lock 1436 non-null int64 29 Powered_Windows 1436 non-null int64 30 Power_Steering 1436 non-null int64 31 Radio 1436 non-null int64 32 Mistlamps 1436 non-null int64 33 Sport_Model 1436 non-null int64 34 Backseat_Divider 1436 non-null int64 35 Metallic_Rim 1436 non-null int64 36 Radio_cassette 1436 non-null int64 37 Parking_Assistant 1436 non-null int64 38 Tow_Bar 1436 non-null int64 dtypes: int64(36), object(3) memory usage: 437.7+ KB
Below I’ll go through every single column one by one. Therefore I won’t repeat the description of them here, but I’ll provide them on each section.
2 Problem Statement
After some good amount of UX practices I learned my lesson that every research should start with a problem statement. So I had some hypothesis that some features of a car such as air conditioning or powered windows should get more important when the car gets older. Following this I came up with the question below:
“What (feature) becomes more important
(~valuable, pricey) when a car is aging?”
2.1 Setting the boundaries: What is old?
But first, I needed to be sure that this dataset contains information related to that statement. If this would be a real-life study, then that statement should’ve come with more clear direction, like ‘what gets important after 10 (or whatever the business goal is) years?’. Here I had to draw my limits within the dataset itself, because if this particular dataset had only 10% of cars that are older than -say- 3 years old, then it wouldn’t make much sense to study this statement with this set. So I tried different years:
(The column ‘Age_08_04’ represents age in months as in August 2004)
three_years = df[(df.Age_08_04 >= 36)]
four_years = df[(df.Age_08_04 >= 48)]
five_years = df[(df.Age_08_04 >= 60)]
six_years = df[(df.Age_08_04 >= 72)]
three_years_old = len(three_years)
four_years_old = len(four_years)
five_years_old = len(five_years)
six_years_old = len(six_years)
total_cars = len(df)
print(f"Number of cars older than 3 years: {three_years_old}, and they are {three_years_old/total_cars:.2f}%")
print(f"Number of cars older than 4 years: {four_years_old}, and they are {four_years_old/total_cars:.2f}%")
print(f"Number of cars older than 5 years: {five_years_old}, and they are {five_years_old/total_cars:.2f}%")
print(f"Number of cars older than 6 years: {six_years_old}, and they are {six_years_old/total_cars:.2f}%")Number of cars older than 3 years: 1215, and they are 0.85% Number of cars older than 4 years: 1034, and they are 0.72% Number of cars older than 5 years: 754, and they are 0.53% Number of cars older than 6 years: 319, and they are 0.22%
Targetting the 5 years and older cars sounds good, since they cover almost the half of the whole dataset.
2.2 Summary of my Initial Analysis
To be able to explain why I was in need of a new and deeper analysis, I better provide a short summary of the results from that first analysis.
I’ve chosen 7 variables, which estimated below coefficients in the table.*
(*They were slightly different, because the dataset they provided had 1427 rows in total, unlike the original set with 1436 rows.)
|-------------|-----------| | hp | 51.65 | | automatic | 727.40 | | doors | 473.05 | | airco | 2045.85 | | pwr windows | 954.6 | | radio | -39.73 | | tow bar | -1548.8 | (a sample reading of this table would be: every bit of hp would bring 51.65 euros to the price of a car, while having a radio would minus the price by 39.73 euros)
These results were for the whole set. After that, I got the results for the older cars to compare them and at the end I’ve had such questions and notes:
1- I’ve chosen variables that seemed to me to have a potential for a noteworthy-effect on the price, especially for the older cars, but I was not sure how to choose variables accurately.
- Shortly speaking, it’s mostly about the domain-knowledge. One needs a good understanding of the domain and the problem statement as well.
- This time, on this analysis I’ll go through every single column to come up with a better set of variables. I’ll chose them based on the data they carry, rather than relying on my guts.
2- After the comparison, some results made sense but some not. Why having an additional feature like a radio or a tow bar would effect the price negatively?
- For the radio, I’ve had a thesis that it might be caused by people’s expectations for a better feature, like a media screen or a CD player. When I’ve checked them through I’ve understood that I might be right on this. This claim will remain at the end of this analysis as well.
- However for the tow bar, I could not understand the reasons behind. Nor the instructors could. They’ve suggested that this set might be a dummy one. At the end of this analysis I’ll have an explanation how a tow bar can effect the price negatively (and this set indeed could be a real one).
3- Back then I did not realize but changing the variables in the regression model dramatically effects the results. I understood that the digits in the table above are extreme and they get ‘milder’ when other variables are introduced into the equation. I have reached to a sense that some variables are being ‘forced’ to carry the negative effect stronger, if there is no other variables that has also negative effect on the overall price.
- Close to the end of this analysis I’ll demonstrate this as well.
3 EDA & Data Cleaning
Alright, let me roll up my sleeves. The EDA phase will be in three steps:
- First, I’ll check every single column and try to understand the dataset better. Meanwhile I’ll do some necessary cleaning & tidying up. I’ll eliminate some columns that I think won’t serve the problem statement.
- Then, I’ll go deeper and investigate the ones that I could not classify at the first round. I’ll double check the other ones as well.
- Lastly, there will be additional eliminations that will be based on tons of iterations. (This is highly related to the issue that I mentioned above in the 3rd note)
3.1 Basic EDA
This is the first step of the EDA, going through all columns of this dataset.
3.1.1 Id
df.Id.describe()count 1436.000000 mean 721.555014 std 416.476890 min 1.000000 25% 361.750000 50% 721.500000 75% 1081.250000 max 1442.000000 Name: Id, dtype: float64
The Id column starts from 1 and ends at 1442, but this dataset has 1436 rows in total. None of the dataset I’ve came across in internet during my research had those missing 6 rows. It looks like the author at the very beginning dropped them out. Anyway, this column won’t serve my goal.
3.1.2 Model
This column shows the models of the Corollas. It could be interesting to study models and their performances, but without a proper direction it is very hard to cluster them correctly, since there are 319 unique values in there. Besides, the names of the models hold some information that are already available within this dataset, such as engine size or number of doors. This column also won’t be used in the equation.
df.Model.describe()count 1436 unique 319 top TOYOTA Corolla 1.6 16V HATCHB LINEA TERRA 2/3-... freq 109 Name: Model, dtype: object
3.1.3 Price
(Offer Price in Euros)
This is my dependent variable. Let’s check what’s inside.
df.Price.describe()count 1436.000000 mean 10730.824513 std 3626.964585 min 4350.000000 25% 8450.000000 50% 9900.000000 75% 11950.000000 max 32500.000000 Name: Price, dtype: float64
sns.histplot(df["Price"])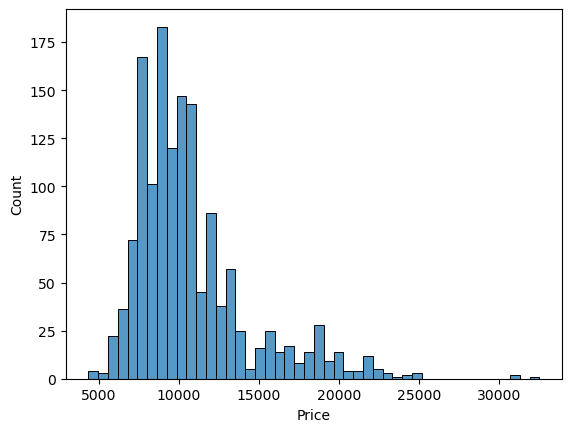
expensive_cars = df[df['Price'] >= 25000]
len(expensive_cars)3
There is only 3 cars that cost more than 25k each and most of the cars are clustered between around 8k-12k euros.
3.1.4 Age
(Age in months as in August 2004)
The name of the column reflects its description. Let me simplify the name first.
df.rename(columns={'Age_08_04':'Age'}, inplace=True)df.Age.describe()count 1436.000000 mean 55.947075 std 18.599988 min 1.000000 25% 44.000000 50% 61.000000 75% 70.000000 max 80.000000 Name: Age, dtype: float64
This dataset has even a one-month-old car, let’s check the distribution. I’ll use years to demonstrate.
x = df["Age"] / 12
plt.xlabel('Years')
sns.histplot(x)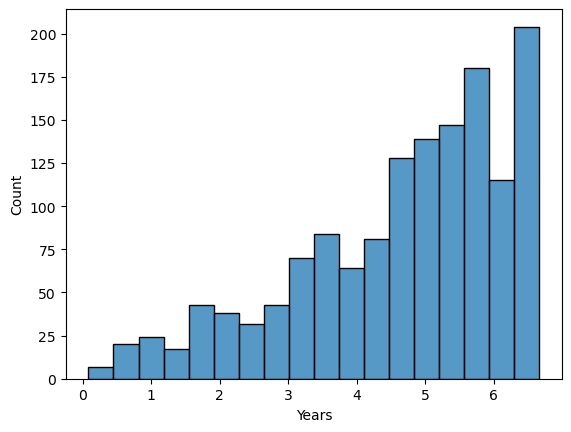
This dataset holds cars that are less than 7 years old and the Age distribution is left skewed.
3.1.5 Mfg_Year & Mfg_Month
(Manufacturing Year & Month)
df.Mfg_Year.describe()count 1436.000000 mean 1999.625348 std 1.540722 min 1998.000000 25% 1998.000000 50% 1999.000000 75% 2001.000000 max 2004.000000 Name: Mfg_Year, dtype: float64
Manufacturing year and month are just a detailed version of the ‘Age’ column, we can say. I just double checked the digits, which look consistent with the ‘Age’. I can continue with the ‘Age’ only, without these two columns.
3.1.6 KM
(Accumulated Kilometers on odometer)
df.KM.describe()count 1436.000000 mean 68533.259749 std 37506.448872 min 1.000000 25% 43000.000000 50% 63389.500000 75% 87020.750000 max 243000.000000 Name: KM, dtype: float64
We have a car that was driven only 1 km, and the KM distribution below is right skewed.
sns.histplot(df["KM"])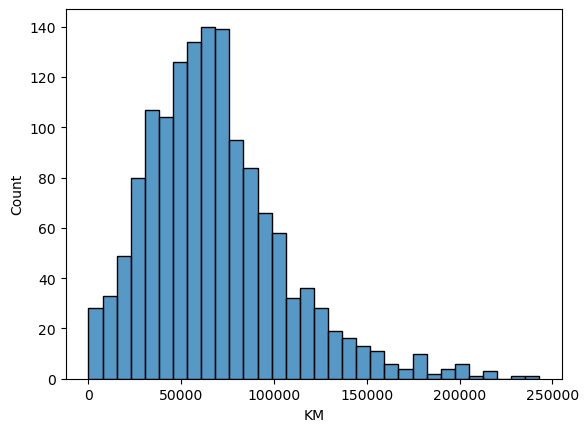
less_used_cars = df[df['KM'] < 10000]
len(less_used_cars)33
We have 11 cars that are less than 1k-km driven and 33 that are less than 10k-km. For this analysis I won’t do anything about the outliers, unless they are indicators of a poor data entry.
3.1.7 Fuel_Type
sns.histplot(df["Fuel_Type"])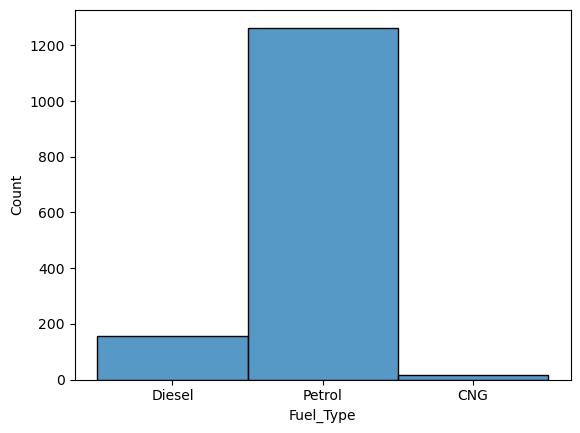
Unfortunately this is the only column about the fuel. It would be nicer to have information about the fuel consumption. Since the petrol type dominates this field, it won’t be helpful to consider this column for older and newer cars seperately, simply bacause the values wouldn’t be fairly distributed.
3.1.8 HP
(Horse Power)
df.HP.describe()count 1436.000000 mean 101.502089 std 14.981080 min 69.000000 25% 90.000000 50% 110.000000 75% 110.000000 max 192.000000 Name: HP, dtype: float64
sns.histplot(df["HP"])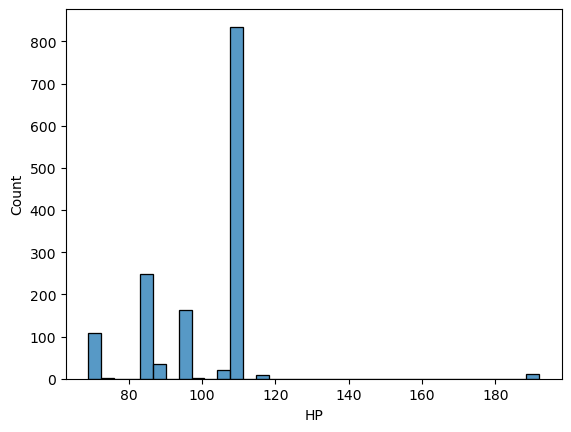
More than half of the cars have 110 hp and mostly they are in less-than-120 range. But there are some very ‘strong’ engines too, let me check them as well, even though I would not touch them.
powered_up = df[df['HP'] > 120]
len(powered_up)11
df.HP.value_counts()110 835 86 249 97 164 72 73 90 36 69 34 107 21 192 11 116 9 98 2 71 1 73 1 Name: HP, dtype: int64
3.1.9 Met_Color
Metallic Color (Yes=1, No=0)
Since this is a boolean type, I’ll skip the chart.
df["Met_Color"].value_counts()1 969 0 467 Name: Met_Color, dtype: int64
Around two-thirds of cars come with a metallic color. For now, I’ll keep them.
3.1.10 Color
Color is a categorical area and I am not sure how I can put it into my numerical MVA. But anyway, it is an interesting topic and color indeed is an important factor for a car, hence its price and probability to be sold fast. I’ll at least check the distribution first.
df["Color"].value_counts()Grey 301 Blue 283 Red 278 Green 220 Black 191 Silver 122 White 31 Violet 4 Yellow 3 Beige 3 Name: Color, dtype: int64
Said those, I am a bit surprized how there are that few white cars in this set. Where I am from, the white color for a car is the top choice and people almost always refer it as “easy to sell color”. Even though, I wouldn’t add ‘color’ into my equation, I’d like to investigate them further. (You’ll see that I’ll have a guess on white color as well.) (A second note: Where I am from or my experiences are not important, every bit of data should be considered within its original context.)
3.1.11 Automatic
Automatic (Yes=1, No=0)
df["Automatic"].value_counts()0 1356 1 80 Name: Automatic, dtype: int64
Considering that this data claims to be collected in 2004, it is not surprizing that automatic gear was not that popular yet. If there would be more cars with automatic gear in this dataset, it would worth to examine, but they are so few to be considered.
(After bunch of iterations I’ll put this column back in the equation. I’ll mention about this on further steps.)
3.1.12 CC
(Cylinder Volume in cubic centimeters)
df.CC.describe()count 1436.00000 mean 1576.85585 std 424.38677 min 1300.00000 25% 1400.00000 50% 1600.00000 75% 1600.00000 max 16000.00000 Name: CC, dtype: float64
That max amount is obviously not a valid input. But let’s check how many we have such high values.
high_cc = df[df['CC'] > 1600]
len(high_cc)167
That’s a lot. Let’s check what’s within those 167 cars.
df[df['CC'] > 1600].CC.describe()count 167.000000 mean 2048.892216 std 1087.889163 min 1800.000000 25% 1900.000000 50% 2000.000000 75% 2000.000000 max 16000.000000 Name: CC, dtype: float64
Looks like the highest volume is 2000, without that 16k. Let’s check this one out.
high_cc = df[df['CC'] > 2000]
len(high_cc)1
Yes it is. It looks like 16k is a typo. Let’s correct it.
df['CC'] = df['CC'].replace(16000, 1600)df.CC.describe()count 1436.000000 mean 1566.827994 std 187.182436 min 1300.000000 25% 1400.000000 50% 1600.000000 75% 1600.000000 max 2000.000000 Name: CC, dtype: float64
Looks good, but let me investigate deeper.
df["CC"].value_counts()1600 846 1300 248 1400 164 2000 119 1900 30 1800 14 1598 4 1587 4 1995 2 1398 2 1332 2 1975 1 Name: CC, dtype: int64
When we talk about the volume of an engine, we don’t need to count every single CC (at least for such analysis). That’s why, those volumes (that are listed above under 1800) can easily be transformed to the nearest 100s.
df["CC"] = df["CC"].round(-2)df["CC"].value_counts()1600 854 1300 250 1400 166 2000 122 1900 30 1800 14 Name: CC, dtype: int64
That looks far better, let’s check the graph too.
sns.histplot(df["CC"])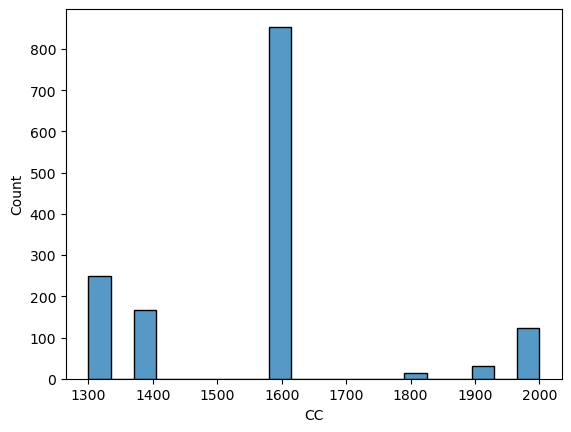
3.1.13 Doors
(Number of doors)
The number of doors, here, I believe can be taken as the indicator for the size of the car. Let’s check how many options we have.
sns.histplot(df["Doors"])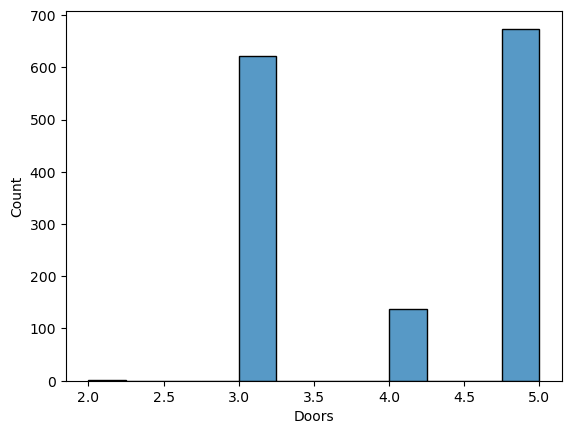
df["Doors"].value_counts()5 674 3 622 4 138 2 2 Name: Doors, dtype: int64
I don’t know what’s the difference between the 2 and 3 door cars but I won’t try to find this one out, since we have only two of them. I’ll keep this column into my equation for checking the size’s effect on the price.
3.1.14 Cylinders
(Number of cylinders)
df["Cylinders"].value_counts()4 1436 Name: Cylinders, dtype: int64
All of the cars have 4 cylinders. I don’t need them in my equation.
3.1.15 Gears
(Number of gear positions)
df["Gears"].value_counts()5 1390 6 43 3 2 4 1 Name: Gears, dtype: int64
Similar to not-having-an-automatic gear, the gears column is also dominated by one value. Almost all cars have 5 gear positions, so it won’t help me much to consider them to compare older and newer cars.
3.1.16 Quarterly_Tax
(Quarterly road tax in Euros)
df.Quarterly_Tax.describe()count 1436.000000 mean 87.122563 std 41.128611 min 19.000000 25% 69.000000 50% 85.000000 75% 85.000000 max 283.000000 Name: Quarterly_Tax, dtype: float64
df["Quarterly_Tax"].value_counts()85 613 69 559 185 96 19 72 100 19 234 19 210 18 64 18 197 14 283 3 72 3 163 1 40 1 Name: Quarterly_Tax, dtype: int64
sns.histplot(df["Quarterly_Tax"])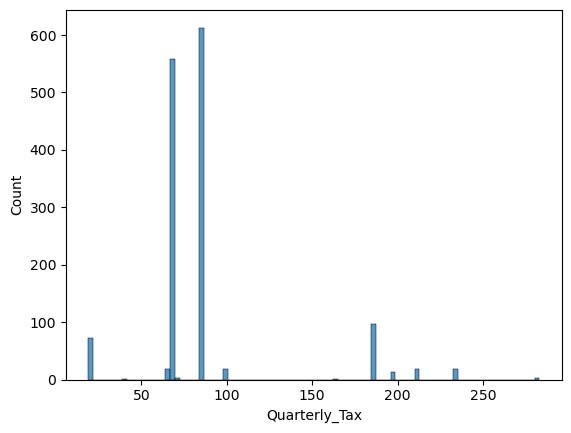
I am not sure how to accurately read the tax issues, since it is not in my area of expertise. But I am also sure that tax is a strong factor to choose and value a car. While being skeptic about this column, I’ll consider it once again in the further investigation below.
3.1.17 Weight
(Weight in Kilograms)
df.Weight.describe()count 1436.00000 mean 1072.45961 std 52.64112 min 1000.00000 25% 1040.00000 50% 1070.00000 75% 1085.00000 max 1615.00000 Name: Weight, dtype: float64
Standard deviation is not high, it means data points are close to the mean. Let’s check the plot too.
sns.histplot(df["Weight"])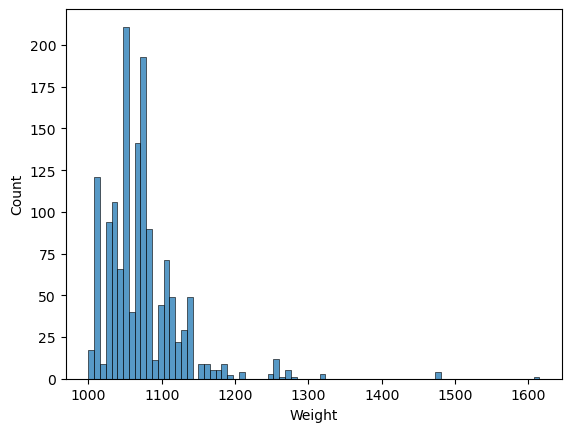
Most of us won’t talk about how much our cars weight, unless its a truck or a heavy-duty vehicle. So it was not the first thing that I think of when I choose a car, but the size and the engine volume directly effects the weight of a car. The above plot also shows varied amounts of weights, so it could be wise to consider this as well.
3.1.18 Mfr_Guarantee
Within Manufacturer’s Guarantee period (Yes=1, No=0)
df["Mfr_Guarantee"].value_counts()0 848 1 588 Name: Mfr_Guarantee, dtype: int64
Similar to the tax-issues, the insurance & guarantee are the topics that needs deep understanding, because there are other factors than the car itself. However above digits show that there are good amount of cars that are within manufacturer’s guarantee. It can be wise to investigate this, so I’ll come to this one in further investigation again.
3.1.19 BOVAG_Guarantee
BOVAG (Dutch dealer network) Guarantee (Yes=1, No=0)
df["BOVAG_Guarantee"].value_counts()1 1286 0 150 Name: BOVAG_Guarantee, dtype: int64
It looks like this dealer provides guarantee for most of the cars. I am not a sales-person but this seems a standard offer for most of the dealers. Again, the distribution is not varied, it doesn’t seem to help my problem statement.
3.1.20 Guarantee_Period
(Guarantee period in months)
df.Guarantee_Period.describe()count 1436.000000 mean 3.815460 std 3.011025 min 3.000000 25% 3.000000 50% 3.000000 75% 3.000000 max 36.000000 Name: Guarantee_Period, dtype: float64
df["Guarantee_Period"].value_counts()3 1274 6 77 12 73 24 4 36 4 18 1 13 1 20 1 28 1 Name: Guarantee_Period, dtype: int64
This shows that most of the guarantee are only for three months. This may be reflecting the dealer’s ‘standard’ offer, as I stated above. But let’s check this one too.
dealers_guar = df[(df['BOVAG_Guarantee'] == 1) & (df['Guarantee_Period'] == 3)]
len(dealers_guar)1193
As we can see only less than 100 cars (out of those in the 3-months-guarantee-period) are not under the dealer’s offer. Since these two columns are highly related to each other and come with a dominant value each, I’ll omit them in my equation.
3.1.21 ABS
Anti-Lock Brake System (Yes=1, No=0)
df["ABS"].value_counts()1 1168 0 268 Name: ABS, dtype: int64
A good amount of Corollas were equipped with ABS even in 2004. While the distribution is not promising, I anyway want to consider this column in my model just to check the safety measures too.
3.1.22 Airbag_1
Driver Airbag (Yes=1, No=0)
df["Airbag_1"].value_counts()1 1394 0 42 Name: Airbag_1, dtype: int64
3.1.23 Airbag_2
Passenger Airbag (Yes=1, No=0)
df["Airbag_2"].value_counts()1 1038 0 398 Name: Airbag_2, dtype: int64
It looks like that the airbags were already standard for driver but not for passengers. The second one can be considered with ABS together for safety choices.
3.1.24 Airco
Air conditioning (Yes=1, No=0)
df["Airco"].value_counts()1 730 0 706 Name: Airco, dtype: int64
Almost half of the cars had air conditioning. This is a good spread of data, so I’ll put this one in the bucket as well.
3.1.25 Automatic_airco
Automatic Airconditioning (Yes=1, No=0)
df["Automatic_airco"].value_counts()0 1355 1 81 Name: Automatic_airco, dtype: int64
Looks like only 81 out of those 730 cars airco are automatic, but I’ll check the consistency of the dataset anyway.
airco_proof = df[(df['Airco'] == 0) & (df['Automatic_airco'] == 1)]
len(airco_proof)0
It looks cool. Let’s continue with Airco only.
3.1.26 Boardcomputer
Board computer (Yes=1, No=0)
df["Boardcomputer"].value_counts()0 1013 1 423 Name: Boardcomputer, dtype: int64
I guess Board computer refers to the driver’s front panel which displays informations (such as fuel consumption, mileage, etc.), rather than the media screen in the middle of the front seats. But since they might be related to each other, I’ll call this column together with other three below (CD Player, Radio and Radio Cassette) as MMDs (multi-media display). As I explained at the beginning (2.2 Summary of my Initial Analysis) about the issues with the ‘radio’ values in my initial analysis, probably I’ll choose one (or max two) of these columns to be considered.
3.1.27 CD_Player
CD Player (Yes=1, No=0)
df["CD_Player"].value_counts()0 1122 1 314 Name: CD_Player, dtype: int64
As stated above, this one goes into the MMD section for now.
3.1.28 Central_Lock
Central Lock (Yes=1, No=0)
df["Central_Lock"].value_counts()1 833 0 603 Name: Central_Lock, dtype: int64
Central lock and the powered windows (below) both have a good distribution to be considered.
3.1.29 Powered_Windows
Powered Windows (Yes=1, No=0)
df["Powered_Windows"].value_counts()1 807 0 629 Name: Powered_Windows, dtype: int64
3.1.30 Power_Steering
Power Steering (Yes=1, No=0)
df["Power_Steering"].value_counts()1 1404 0 32 Name: Power_Steering, dtype: int64
Again, it seems that having a power steering is a default feauture already. I won’t put it into the equation.
3.1.31 Radio
Radio (Yes=1, No=0)
df["Radio"].value_counts()0 1226 1 210 Name: Radio, dtype: int64
Goes into the MMD basket.
3.1.32 Mistlamps
Mist lamps (Yes=1, No=0)
df["Mistlamps"].value_counts()0 1067 1 369 Name: Mistlamps, dtype: int64
Around a quarter of cars have mist lamps. Let’s consider them too.
3.1.33 Sport_Model
Sport Model (Yes=1, No=0)
df["Sport_Model"].value_counts()0 1005 1 431 Name: Sport_Model, dtype: int64
Comparing to the other engine-related values like gear or volume (cc), this one seemed to me more abstract. Also the domain-knowledge plays a good role here: What is a sport model for this particular brand and model? It can be upgrade for the engine or for the outlook or for both. In my experience, in most cases it indicates some additions to the outer look of the car. So it is an effort to make the car ‘look’ like sportive, rather than ‘act’ like so. But my experience is not important, this specific car/model is essential here.
With this ambiguity I tend not to consider this deeply. But I’ll anyway investigate this in further steps below, because a good amount of cars come with sport model as the above digits reflect.
3.1.34 Backseat_Divider
Backseat Divider (Yes=1, No=0)
df["Backseat_Divider"].value_counts()1 1106 0 330 Name: Backseat_Divider, dtype: int64
A fun fact: For couple of times I was reading this as ‘backseat driver’ and was thinking how interesting and cool this dataset was.
But unfurtunately, this is the same old, boring thing, called a divider. Probably it is the armrest (cupholder) in the middle of the backseats, but it can also mean that the backseats are foldable. I don’t know, and again I don’t want to guess also. Obviously such things cost money but I am not sure the overall effect on the entire car price or how it can effect one while choosing an older car. Yet, let’s keep it for further study anyway.
3.1.35 Metallic_Rim
Metallic Rim (Yes=1, No=0)
df["Metallic_Rim"].value_counts()0 1142 1 294 Name: Metallic_Rim, dtype: int64
I have similar concerns for this one too as I stated above. Not sure how this can effect the price of an older car but almost 300 cars have metallic rims, so let’s keep them in the basket until further investigation.
3.1.36 Radio_cassette
Radio Cassette (Yes=1, No=0)
df["Radio_cassette"].value_counts()0 1227 1 209 Name: Radio_cassette, dtype: int64
This one is the last column of the above-stated MMDs and it’s very close to the results for ‘Radio’, which only 210 cars have. Let’s check how many cars have both.
radio_gaga = df[(df['Radio'] == 1) & (df['Radio_cassette'] == 1)]
len(radio_gaga)208
Looks like they are representing same set of things (radio + cassette player). So putting them in the same basket (multi-media displays) doesn’t sound as a bad idea.
Though, I understand that 2 cars having only radio without cassette player, but I don’t understand the one car that has cassette player but without a radio. That is odd. Maybe that one’s radio was broken, I don’t know. If so, then I have to put one side note here:
💡 For every boolean value, how can we be sure that they all value equally? How can we calculate those nuances within each variable? Or should we at all?
3.1.37 Parking_Assistant
Parking Assistant System (Yes=1, No=0)
df["Parking_Assistant"].value_counts()0 1432 1 4 Name: Parking_Assistant, dtype: int64
It looks like back then parking assistant was in the luxury zone, at least for these Corollas. It wouldn’t give us much to add them in the equation.
(In fact, a lot of datasets in the web, that are titled Corolla dataset, don’t have this column at all. They were dropped as default.)
3.1.37 Tow_Bar
Tow Bar (Yes=1, No=0)
df["Tow_Bar"].value_counts()0 1037 1 399 Name: Tow_Bar, dtype: int64
For me, the most interesting column is this tow bar. My initial analysis which revealed that tow bar’s negative effect on the price made me go that much deep into this dataset once again. It is definetely in my equation, more reasoning will come after.
3.1.38 The Summary of the Basic EDA
Ok, that was a long journey. I need a summary here. In the table below, strikethrough names represent eliminated columns, bold ones to be considered as independent variables (will be double checked with further EDA anyway) and italic ones to be investigated further.
(Spoiler Alert: This won’t be the final list.)
| Doors | Boardcomputer | |
| CD_Player | ||
| Price | Central_Lock | |
| Age | Quarterly_Tax | Powered_Windows |
| Weight | ||
| Mfr_Guarantee | Radio | |
| KM | Mistlamps | |
| Sport_Model | ||
| HP | ABS | Backseat_Divider |
| Met_Color | Metallic_Rim | |
| Color | Airbag_2 | Radio_cassette |
| Airco | ||
| CC | Tow_Bar |
3.2 Further EDA
On this second step, I’ll check the relationships of the columns between each other and perform one more elimination phase.
3.2.1 Color
Before I go deep into a correlation matrix, let’s get the colors done first. Again, I won’t integrate a variable such as color into this MVA equation. But I anyway want to examine how cars’ colors act on the price.
With that many color options, histogram looks a bit messy, so I’ll try KDE (kernel density estimation) instead.
palette ={"Grey": 'grey', "Blue": 'blue', "Red": 'red', "Green": 'green', "Black": 'black', "Silver": 'silver', "White": 'white', "Violet": 'violet', "Yellow": 'yellow', "Beige": 'beige',}
sns.displot(df, x="Price", hue="Color", kind="kde", multiple="stack", palette=palette)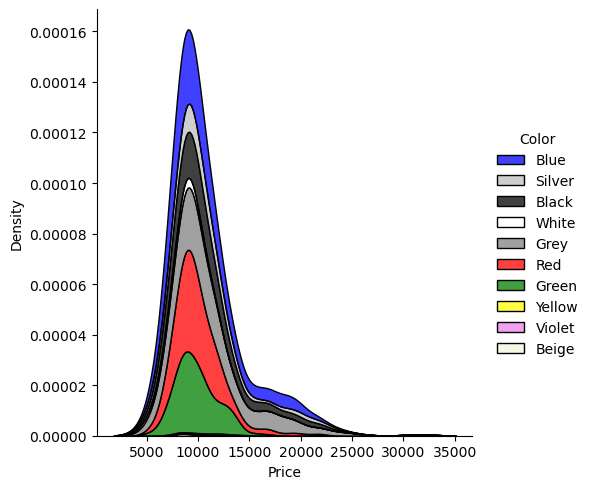
These results are interesting, let’s remember how the colors were distributed.
df["Color"].value_counts()Grey 301 Blue 283 Red 278 Green 220 Black 191 Silver 122 White 31 Violet 4 Yellow 3 Beige 3 Name: Color, dtype: int64
Looks like blue, silver and black ones are the most popular ones. The most frequent color grey comes even after white. Maybe my comment on white color (at the beginning of the study: 3.1.10 Color) fits here as well. There are only 31 of them, yet they have a higher density here.
💡 Another point of view: Maybe white car owners don’t want to trade their cars, and keep them to themselves. Who knows?
For the moment, I’ll stop here with the ‘color’ column and I won’t consider them to serve my problem statement. These color options may be studied deeper in another analysis.
3.2.2 Correlation Matrix
Let’s check the correlation matrix without the eliminated columns.
plt.figure(figsize=(16, 14))
df_filtered = df.filter(['Age', 'KM', 'HP', 'Met_Color', 'CC', 'Doors', 'Quarterly_Tax', 'Weight', 'Mfr_Guarantee', 'ABS', 'Airbag_2', 'Airco', 'Boardcomputer', 'CD_Player', 'Central_Lock', 'Powered_Windows', 'Radio', 'Mistlamps', 'Sport_Model', 'Backseat_Divider', 'Metallic_Rim', 'Radio_cassette', 'Tow_Bar', 'Price'], axis=1)
corr = df_filtered.corr()
sns.heatmap(corr, annot=True, cmap='coolwarm', square=True)
plt.title('Correlation Matrix')
plt.show()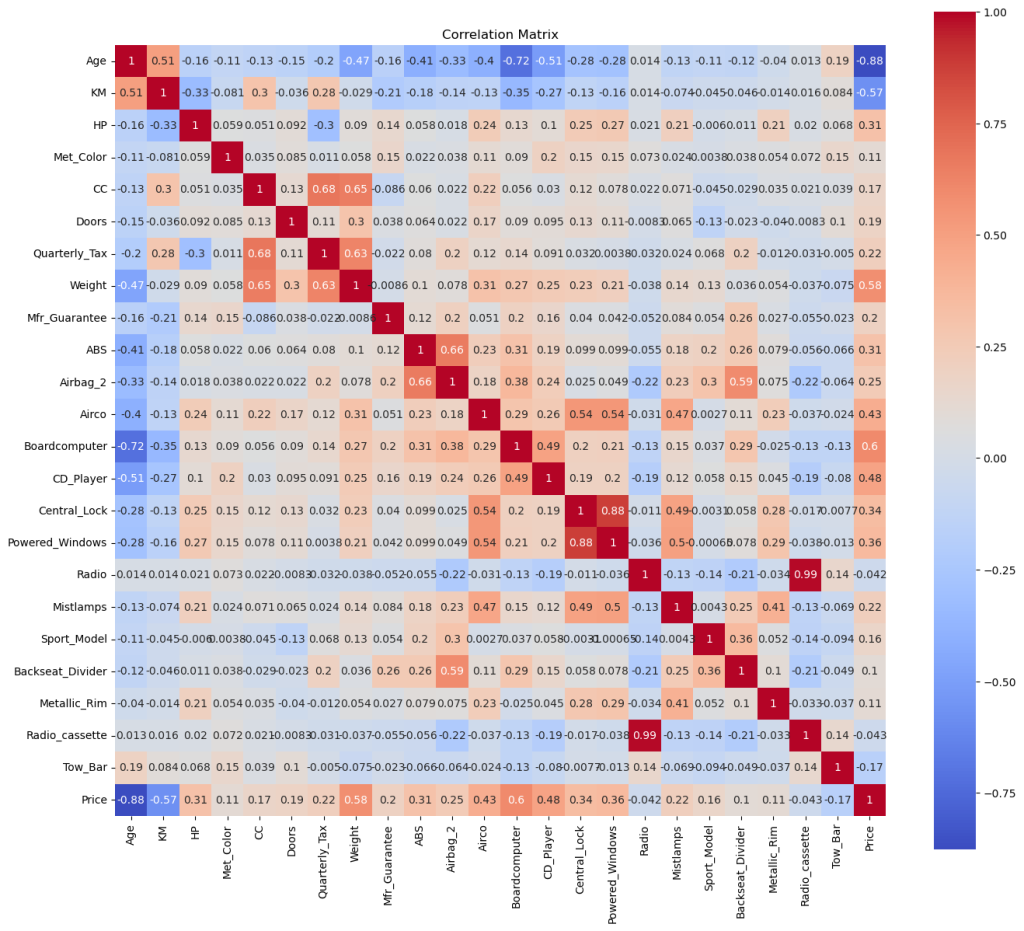
Let me continue with my notes by clustering the related features together:
3.2.3 Condition
Age and KM have the strongest negative correlation between them and the price. I’ll keep them for sure.
3.2.4 Characteristics
We don’t have fuel consumption, but we have HP and CC. So they can be considered for the engine. Doors and Weight on the other side can be considered for the size of the car. I was not sure about the weight, but it has a strong positive relation with the price. They are in.
3.2.5 Interior & MMDs
As I mentioned earlier Radio and Radio Cassette has a strong relation with each other, though their effect on price is low and negative. My counter argument (that people’s expactations for a better system) might be true, considering the strong correlation of Board Computer and CD Player. Board Computer could be enough alone, but let’s keep them both in, while taking the radios out. / Aircondition also has a strong relation, so it’s still in.
3.2.6 Features
Central Lock and Powered Windows have one of the strongest relationship between each other, which makes sense. Mostly they are connected to the same system. As you may noticed in some cars, holding longer to the lock key also rolls up the windows to close them. For the simplicity, we can keep only one of them. Say, the Powered Windows with a slightly higher correlation between it and the price. / Tow Bar, having the thirdest strongest negative correlation will be definetely in the equation and Mistlamp too is still in.
3.2.7 Exterior & Sport Model
I was thinking the Sport Models are offering some upgrades on exterior. But the matrix shows very weak relations between the sport model and the metallic rim, metallic color and also mist lamps (those are the only features I can think of as the exterior). However, the correlations between sport model and Backseat Divider, Passenger Airbag and ABS are stronger. Maybe after all, having a sport model (of these Corollas) means to have something more inside the car. Considering the weak correlation of Backseat Divider, I’ll continue with the Sport Model only (not sure though, because its correlation is also not strong with 0.16), while eliminating the divider. But let’s try to back this one up with the data itself:
df["Sport_Model"].value_counts()0 1005 1 431 Name: Sport_Model, dtype: int64
sport_or_not = df[(df['Sport_Model'] == 1) & (df['Backseat_Divider'] == 1)]
len(sport_or_not)431
This shows that all sport models comes with the backseat dividers. Let’s continue with the decision above. But since this sport model seems to be not related to the exterior, I’d still like to consider some outlook features. Despite the weak correlation of Metallic Rim and Metallic Color (both 0.11), I’ll give them a try.
3.2.8 Safety
ABS and Passenger Airbag‘s correlations are promising, I’ll keep them into the equation and it’s also good to have something about safety.
3.2.9 Others
I’ll eliminate the Quarter Tax, because unlike the other columns, it is affected by the price itself, not the other way around. / Although I am not quite sure about the guarantee, I’ll consider Manufacturer’s Guarantee as well. It has not so weak correlation and for most of us it is an important factor, especially when it comes to the older cars. But first I need to be sure that we have enough old cars within such guarantee.
sns.histplot(df, x="Age", hue="Mfr_Guarantee", element="step")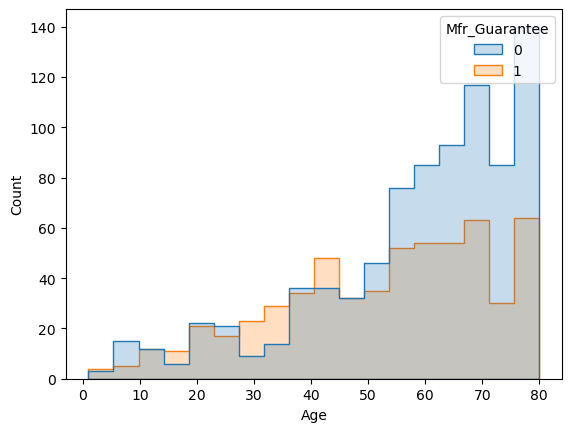
Despite the fact that only around one-third of the older cars are under the guarantee, this is still not a bad distribution. Let’s check the counts as well.
guar_for_old = df[(df['Mfr_Guarantee'] == 1) & (df['Age'] >= 60)]
len(guar_for_old)255
len(guar_for_old) / df["Mfr_Guarantee"].sum()0.4336734693877551
Among older cars 255 of them have guarantee and they are around 43% of the whole cars that are under such guarantee. This digits are not bad, so I’ll stick with my decision.
3.2.10 The Summary of the Further EDA
Let’s replot the correlation matrix after the second elimination, which will serve as a summary as well. This time I’ll keep the order of those clusters above.
plt.figure(figsize=(14, 12))
df_study = df.filter(['Age', 'KM', 'HP', 'CC', 'Doors', 'Weight', 'Boardcomputer', 'CD_Player', 'Airco', 'Powered_Windows', 'Tow_Bar', 'Mistlamps', 'Sport_Model', 'Metallic_Rim', 'Met_Color', 'ABS', 'Airbag_2', 'Mfr_Guarantee', 'Price'], axis=1)
corr_study = df_study.corr()
sns.heatmap(corr_study, annot=True, cmap='coolwarm', square=True)
plt.title('Correlation Matrix')
plt.show()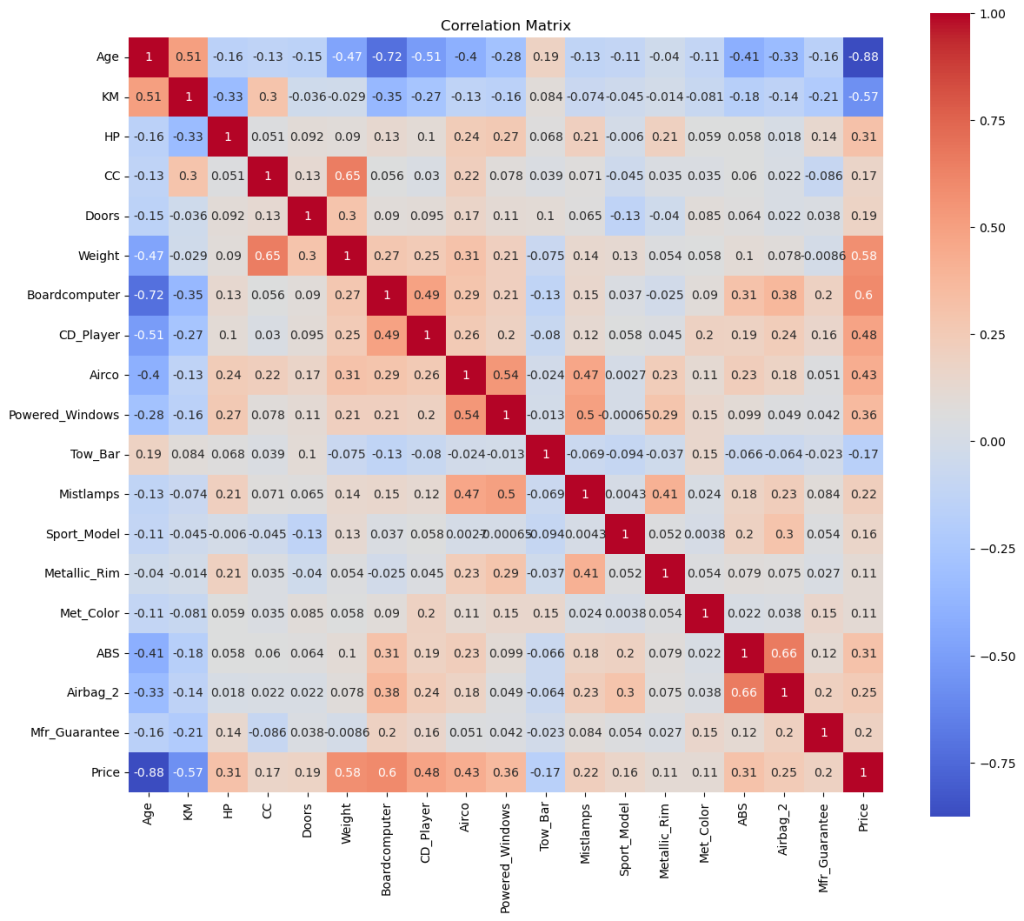
3.3 A Thousand Hidden Steps
People from the UX Design field are very well aware of the iterative structure of their work. This goes here as well. I had to come back and go forward countless times and this exact place was the peak point of those movements. I had to try a huge amount of sets (of variables) to come up with the best fitted combination to this particular model. That’s why my final set of independent variables became different than stated above. For the sake of the simplicity of the flow, I’ll just list the final variables below. At the end, I’ll come back to this ‘hidden steps’ and try my best to provide some feedback on this final elimination phase.
3.3.1 Final Variables
- Age
- KM
- HP
- Automatic
- Doors
- Mfr_Guarantee
- Airco
- CD_Player
- Powered_Windows
- Mistlamps
- Sport_Model
- Metallic_Rim
- Tow_Bar
4 Linear Regression
import sklearn
from sklearn import linear_model4.1 Remembering the Initial Analysis
Before I jump into the final variables, I’d like to re-assign the ones from the very first analysis. As I explained at the beginning (2.2 Summary of my Initial Analysis) this time Age and KM will be added too, just to check the effects when they are into the equation. Remember, they were carrying the strongest negative correlation to the price.
y= df['Price'].values
X_init= df[['Age', 'KM', 'HP', 'Automatic', 'Doors', 'Airco', 'Powered_Windows', 'Radio', 'Tow_Bar']].valuesregr_init = linear_model.LinearRegression()
regr_init.fit(X_init, y)# Getting the coefficiencies with a formatter to better read.
np.set_printoptions(formatter={'float_kind':'{:.2f}'.format})
# Rounding to two decimal points.
print(np.around(regr_init.coef_,2))[-145.95 -0.01 30.84 756.35 186.71 261.61 473.17 -243.02 -243.04]
Let me put the results into a table for a better readability. First columns show the above digits, the next one reflects the initial ones. As it can be seen, the changes can be strong.
|-------------|-------------|-----------| | age | -145.95 | X | | km | -0.01 | X | | hp | 30.84 | 51.65 | | automatic | 756.35 | 727.40 | | doors | 186.71 | 473.05 | | airco | 261.61 | 2045.85 | | pwr windows | 473.17 | 954.6 | | radio | -243.02 | -39.73 | | tow bar | -243.04 | -1548.8 |
Ok, maybe this is obvious for a data scientist but for someone like me at the entry-level, this was one of those moments where I realized the importance of choosing the ‘right’ variables, deciding the ‘accurate’ models/methods and the relationship between these two. This is where I got lost in those hidden steps that I mentioned above. (I’ll come back to this again.)
4.2 Assigning the Variables
Here I am setting the independent variables for the whole set.
y= df['Price'].values
X_study= df[['Age', 'KM', 'HP', 'Automatic', 'Doors', 'Mfr_Guarantee', 'Airco', 'CD_Player', 'Powered_Windows', 'Mistlamps', 'Sport_Model', 'Metallic_Rim', 'Tow_Bar']].valuesregr_study = linear_model.LinearRegression()
regr_study.fit(X_study, y)print(np.around(regr_study.coef_,2))[-141.84 -0.01 28.97 747.43 234.85 105.66 159.77 251.05 346.62 366.15 633.44 136.67 -201.59]
4.2.1 Linear Model for Older and Newer Cars
Here I am doing the same for the older (5 or more years) and -this time also- for the newer (less than 5 years) cars, by hoping to have deeper insights.
older_cars = df[(df.Age >= 60)]
newer_cars = df[(df.Age < 60)]y= older_cars['Price'].values
X_older= older_cars[['Age', 'KM', 'HP', 'Automatic', 'Doors', 'Mfr_Guarantee', 'Airco', 'CD_Player', 'Powered_Windows', 'Mistlamps', 'Sport_Model', 'Metallic_Rim', 'Tow_Bar']].valuesregr_older = linear_model.LinearRegression()
regr_older.fit(X_older, y)print(np.around(regr_older.coef_,2))[-82.64 -0.01 2.45 536.67 199.53 275.87 304.95 96.71 261.91 122.65 -48.28 96.70 -207.86]
y= newer_cars['Price'].values
X_newer= newer_cars[['Age', 'KM', 'HP', 'Automatic', 'Doors', 'Mfr_Guarantee', 'Airco', 'CD_Player', 'Powered_Windows', 'Mistlamps', 'Sport_Model', 'Metallic_Rim', 'Tow_Bar']].valuesregr_newer = linear_model.LinearRegression()
regr_newer.fit(X_newer, y)print(np.around(regr_newer.coef_,2))[-188.08 -0.01 42.31 656.38 216.53 122.24 296.26 90.35 97.82 774.85 723.78 281.02 16.83]
Before I put all these digits into a table, I’ll get the average price for all mentioned age groups too. Because comparing the results alone wouldn’t reflect their proportions within the groups.
avg_all = df['Price'].mean()
avg_older = older_cars['Price'].mean()
avg_newer = newer_cars['Price'].mean()
print(f"Average price for all cars: {avg_all:.2f} €")
print(f"Average price for older cars: {avg_older:.2f} €")
print(f"Average price for newer cars: {avg_newer:.2f} €")Average price for all cars: 10730.82 € Average price for older cars: 8586.91 € Average price for newer cars: 13101.07 €
5 Results
All results are collected below. First two columns (after the names) represents the digits for all cars, the middle two are for older cars (my target as stated in the problem statement), and the last two shows digits for cars that are less than 5 years old, just to read the results in a wider perspective.
Let’s inspect them all one by one. (And when I say ‘car’, I mean a ‘Toyota Corolla’ that is within this particular dataset.)
| all | 10730.82 | older | 8586.91 | newer | 13101.07 | |
|---|---|---|---|---|---|---|
| Age | -141.84 | -1.32% | -82.64 | -0.96% | -188.08 | -1.44% |
| KM | -0.01 | -0.01 | -0.01 | |||
| HP | 28.97 | 0.27% | 2.45 | 0.03% | 42.31 | 0.32% |
| Automatic | 747.43 | 6.97% | 536.67 | 6.25% | 656.38 | 5.01% |
| Doors | 234.85 | 2.19% | 199.53 | 2.32% | 216.53 | 1.65% |
| Mfr_Guarantee | 105.66 | 0.98% | 275.87 | 3.21% | 122.24 | 0.93% |
| Airco | 159.77 | 1.49% | 304.95 | 3.55% | 296.26 | 2.26% |
| CD_Player | 251.05 | 2.34% | 96.71 | 1.13% | 90.35 | 0.69% |
| Powered_Windows | 346.62 | 3.23% | 261.91 | 3.05% | 97.82 | 0.75% |
| Mistlamps | 366.15 | 3.41% | 122.65 | 1.43% | 774.85 | 5.91% |
| Sport_Model | 633.44 | 5.90% | -48.28 | -0.56% | 723.78 | 5.52% |
| Metallic_Rim | 136.67 | 1.27% | 96.7 | 1.13% | 281.02 | 2.15% |
| Tow_Bar | -201.59 | -1.88% | -207.86 | -2.42% | 16.83 | 0.13% |
5.1 Age
These results look like the proof of that saying “Your car started to lose the value the moment you bought it.” The effect gets weaker with more than 5 years old cars, but it is still effecting the price of the car negativetely. We might have deeper understanding if we had cars -say- more than 10 years old too. Then we could check the effects after a certain age as well.
5.2 KM
This is the only variable that had the same effect on each age-group. No matter how old your car is, mileage ‘damages’ the value more or less the same. Though these same results made me question one more thing:
If we check the digits for all cars, we can say that a car getting-one-month-old costs us around 140 Euro. But to lose 100 Euro we need to drive 10k km, according to these digits. So driving 14k km ‘damages’ the value equally as the car gets just 1-month old, which is not logical at all.
When I try other set of variables (remember those hidden steps), KM always get me either -0.01 or -0.02. Even if I’ll calculate with the later one, driving 7k km, imho*, should costs us more than getting-a-month-older car.
💡 I can think of two things: There might be some other dynamics that this model could not present accurately. Or, the car dealers are really harsh when it comes to evaluate second hand cars and they use the age of an car as one of their strongest arguments to ‘price cut’.
* It's not just my opinion, it's the fact: - According to the Enerdata, the average kilometers per a driver in Europe per year was around 13k in 2004. This dropped down to around 11.3k in 2019.[1] - According to the Federal Highway Administration, the average annual miles per a driver in US in 2000 was around 13.5k (~21.7k km).[2] They also reported that, on average, VMT (Vehicle Miles Traveled) rose by 3.3 percent per year from 1929–2014.[3] - According to Tuik (Turkish Statistical Institute), the average annual kilometers per a driver in Turkiye in 2020 was around 14k.[4]
5.3 HP
| all | 10730.82 | older | 8586.91 | newer | 13101.07 | |
|---|---|---|---|---|---|---|
| HP | 28.97 | 0.27% | 2.45 | 0.03% | 42.31 | 0.32% |
It seems that having a ‘strong’ engine does not help you to sell your older Corolla. Comparing to the overall and also the newer cars, HP loses its value around 90%.
5.4 Automatic
| all | 10730.82 | older | 8586.91 | newer | 13101.07 | |
|---|---|---|---|---|---|---|
| Automatic | 747.43 | 6.97% | 536.67 | 6.25% | 656.38 | 5.01% |
No matter how old your car is, having an automatic gear is a valuable thing. I am aware that I need to be careful here, because we don’t have much cars with an automatic gear in this dataset. But as I’ll explain below (6.3 Automatic Gear) the reflective distribution helps me to say so. Besides, considering that this dataset is from 2004 and how automatic cars are popular now,
💡 maybe we can safely claim that there was a demand towards this direction even that time.
5.5 Doors
| all | 10730.82 | older | 8586.91 | newer | 13101.07 | |
|---|---|---|---|---|---|---|
| Doors | 234.85 | 2.19% | 199.53 | 2.32% | 216.53 | 1.65% |
If we can read the number of doors as an indicator for the size of the car, we can also tell by checking this result that the size of the car is an important factor for all ages. In fact, if we check the percentages (to the mean of the price) its effects gets stronger on older cars.
💡 Maybe we can claim that asking for a bigger car is more common among cars that are older than 5 years.
5.6 Mfr_Guarantee
| all | 10730.82 | older | 8586.91 | newer | 13101.07 | |
|---|---|---|---|---|---|---|
| Mfr_Guarantee | 105.66 | 0.98% | 275.87 | 3.21% | 122.24 | 0.93% |
This was a hypothesis that I wanted to test and the results proofed it. No surprize here, if your car is under manufacturer’s guarantee, you can value it higher. It is even more important for the older cars.
5.7 Airco
| all | 10730.82 | older | 8586.91 | newer | 13101.07 | |
|---|---|---|---|---|---|---|
| Airco | 159.77 | 1.49% | 304.95 | 3.55% | 296.26 | 2.26% |
As it was with the guarantee, I was expecting that having an air conditioning would mean more for older cars. I am glad that these results reflects this, unlike in my initial analysis. In that study, despite the positive effect on the price, it was less effective compared to the whole cars. Again, I think this was caused by the variable choices.
5.8 CD Player & Powered Windows
| all | 10730.82 | older | 8586.91 | newer | 13101.07 | |
|---|---|---|---|---|---|---|
| CD_Player | 251.05 | 2.34% | 96.71 | 1.13% | 90.35 | 0.69% |
| Powered_Windows | 346.62 | 3.23% | 261.91 | 3.05% | 97.82 | 0.75% |
I was thinking that having powered windows and CD player would be more important when your car is old, like as having an air conditioning. For these, the effect gets weaker compared to all cars. But having a second look at the newer cars, the importance is underlined for older cars.
💡 We can also claim that people who are buying newer cars, already expect to have powered windows (and CD Player) as default, so it’s effect is less strong compared to the older ones.
5.9 Mist Lamps & Metallic Rim
| all | 10730.82 | older | 8586.91 | newer | 13101.07 | |
|---|---|---|---|---|---|---|
| Mistlamps | 366.15 | 3.41% | 122.65 | 1.43% | 774.85 | 5.91% |
| Metallic_Rim | 136.67 | 1.27% | 96.7 | 1.13% | 281.02 | 2.15% |
Mist lamps and Metallic rims were not in my main focus, simply because I was thinking that they won’t serve the problem statement. In fact, the correlation matrix also showed not so strong digits (0.22 and 0.11 respectively) for their relations to the price. I anyway wanted to examine some features about the outlook of the car. We can tell that both add value to your car, but loses their effects when your car is getting older than 5 years.
However, an additional look to the correlation matrix reveals some other things. Check their strongest relations with some other features below.
Mistlamps > Powered Windows (0.59) / Airco (0.47) / Metallic Rim (0.41) Metallic Rim > Mistlamps (0.41) / Powered Windows (0.29) / Airco (0.23)
These numbers show how these are related to each other. This kind of further investigation did shape this analysis much and below you will see other samples.
5.10 Sport Model
| all | 10730.82 | older | 8586.91 | newer | 13101.07 | |
|---|---|---|---|---|---|---|
| Sport_Model | 633.44 | 5.90% | -48.28 | -0.56% | 723.78 | 5.52% |
You may remember how I revealed the relationship between the Sport Model and the Backseat Divider (3.2.7 Exterior & Sport Model). To understand its negative effect on older cars, let’s check the strongest relations as we did above. I’ll add Backseat Divider as well for a wider perspective.
Sport Model > Backseat Divider (0.36) / Airbag_2 (0.3) / ABS (0.2) Backseat Divider > Airbag_2 (0.59) / Sport Model (0.36) / Boardcomputer (0.29) / ABS (0.26) / Mistlamp (0.25)
So Sport Model and all these kind of features may represent some additional packages that car producers offer. And checking the newer (and all) cars results above, we can tell that they are somehow indicating being new. Investigations below will support this view too.
5.11 Tow Bar
| all | 10730.82 | older | 8586.91 | newer | 13101.07 | |
|---|---|---|---|---|---|---|
| Tow_Bar | -201.59 | -1.88% | -207.86 | -2.42% | 16.83 | 0.13% |
This is the most fun part of this analysis for me. After all, the strong but negative effect (on price) of having a tow bar brought me up here. Ok, some other things as well! But unlike other ‘surprizing’ results, tow bar indeed had a negative correlation between the price as the matrix presented. I have to admit that I was not aware of this while working on the initial analysis. This made me question my (and also the instructors) expectations and interpretations (that I mentioned at the beginning in 2.2 Summary of my Initial Analysis).
After spending some time in internet and reading articles titled like “What Are the Dangers of Buying a Car With a Towbar Already Fitted?” and forum posts asking questions like “Towbar take it off or leave it on when trading in?” or “Used cars with tow bars – more risky to buy?“, I’ve come to a conclusion that having a towbar really can decrease the price of a car. Mainly because the dealers tendency to read them as a sign of a car being ‘used roughly’.
Again, it looks like that the importance of domain-knowledge plays an essential role* here. But even so, I need to find some concrete proof within this database to support this thesis. Because even if this is a thing, it might not be a case for our situation.
* Ok, I need one more side note here: Remember my doubt about the Boolean values?: How can they all weight the same? If a dealer checks your car's tow bar just visually and notes it as something 'bad' without further investigation, then my question gets even stronger. Having a tow bar shouldn't mean something, how-it-was-used may be. Remember that old car commercial? (this or this)
Then, I started to dig deeper into the dataset and used similar methods as stated above. Let’s first check how many older cars have tow bar.
tow_old = df[(df['Tow_Bar'] == 1) & (df['Age'] >= 60)]
len(tow_old)253
That’s more than half of the total tow bar cars (we had 399 of them). Let’s check the whole picture.
sns.histplot(df, x="Age", hue="Tow_Bar", element="step")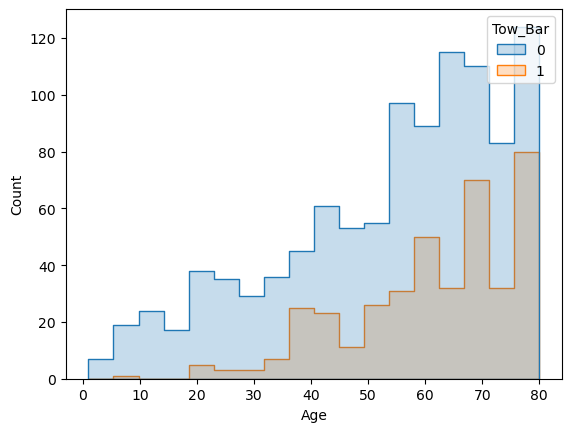
This graph shows clearly that most of the tow bars showing themselves after around 3 years (36 months) and close to 5 years it reaches a point where older cars with a tow bar did not get below that level. So apart from the concerns that were raised in those forums above, here in this particular dataset having a tow bar could mean having an old car too. If they were not coming as a default part of those Corollas, then it could really mean that the owners did ‘touch’ the car in the way that dealers evaluate negatively.
So I think I got my answer to the tow bar question! Or at least for now, I am convinced with what I got.
This brings me to those hidden steps (that I mentioned above in the section 3.3). While trying to figure out the results, I started to try tons of different set of variables to get a wider angle which made me realize the probability of such relationships as I mentioned here. So let me demonstrate some of such investigations from those hidden steps.
6 Coming back to those Hidden Steps
Here I’ll try to explain why I left some more variables out of my equation after the second round of the EDA.
6.1 Board Computer, ABS and Passenger Airbag
In all combinations of my variables these three were giving me negative results. This was unexpected, because all had positive correlation between them and the price (0.6, 0.31 and 0.25 respectively). Considering that the Board Computer had the strongest positive correlation, this became even more interesting. But the matrix also revealed a very strong but negative correlation (-0.72) between the Board Computer and the Age. We need to look at this situation closer.
sns.histplot(df, x="Age", hue="Boardcomputer", element="step")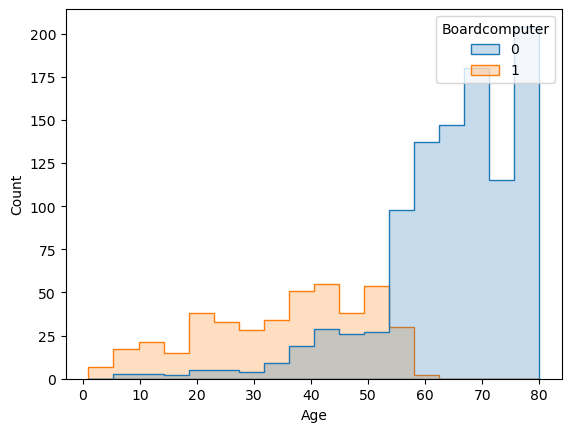
I guess this is the place where I can use that phrase: A picture is worth a thousand words. The cars that don’t have Board Computer start to rise with around 30 months old cars and after 5 years none of the cars have it. So not having a board computer -here- is a very strong indicator of being an old car. A similar pattern can be found with the ABS and the Airbag_2, but not as dramatic as this one. I believe this can be the reason of those negative results when it comes to coefficients. Or, maybe we can claim that their relationships does not fit to a linear model. / That’s why I eliminated these.
6.2 Weight and CC
I wanted to consider both Weight and Doors together to check the effects of the car size. They were giving ‘expected’ results when only one of them were in the list of the variables. However, Doors were giving negative results when the Weight were introduced in. Eliminating Weight was a better fit for this model, but considering their distributions I guess that both were not a good fit for a linear model. / Despite its positive correlation (0.17) the CC column was also not consistent. It might be caused due to the distribution again. Remember that 1600cc was dominating the column (Section 3.1.12).
6.3 Automatic Gear
You may remember that I left the Automatic gear out of my equation in the first round of EDA, because of the ‘poor’ distribution. However on all the iterations that I’ve given a try, they were consistent and positive. That’s why I double checked the situation.
sns.histplot(df, x="Age", hue="Automatic", element="step")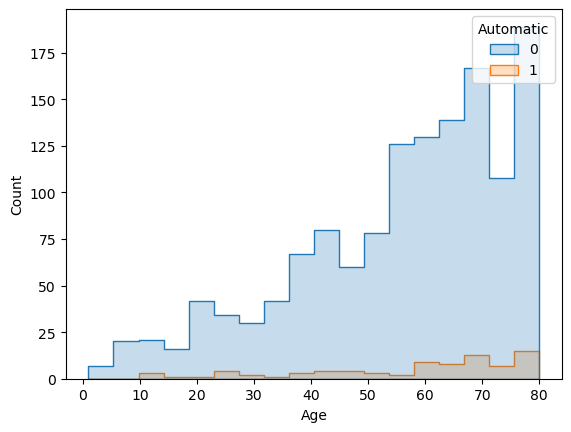
Although it is weak, the non-automatic cars distribution follows similar pattern with the automatic ones. 50 out of 80 automatic cars were over 5 years old. That’s why I kept them in the variables. Said that, I did not do the same for Automatic Air Conditioning, even though it gave very positive digits. Because only 4 out of 81 cars with automatic airco were over 5 years old.
7 Conclusion
Ok, I need an ending, right? If you followed all steps till here, I am grateful to your patience. This is my final note:
If you are a 5-or-6-years-old Corolla owner and the year is 2004 and you want to check this dealer’s offer to trade your car, here is what I can tell you based on the steps above:
7.1 Do These
✅ If the car has an automatic gear, start your bargain with it. Tell them how smoothly it works!
✅ The same goes for your cool air conditioning. (If you did change the filter, you can mention that too. But don’t forget: No data is shown above related to any filter.)
✅ While telling all of these, roll up and down your powered windows. Show them who has the power!
✅ If your car is still under the manufacturer’s guarantee, you should definetely talk about it.
☑️ If you feel the vibe is positive, add some flavors by telling about your mist lamps and metallic rims. But don’t rely on these much.
7.2 Don’t Do These
❌ If your car has a strong engine, better not brag about your horses!
❌ If your car’s sportive outlook is all about that backseat divider, don’t even mention it.
❌ Never, ever think to tell how ‘good’ your car is by reasoning it with its ability to pull heavy trailers with that tow bar. If the dealers use the tow bar as an argument for price cut, tell that you only carried your 5-years-old kid’s bicycle on that. (But again, there is no data above about any kid’s bike)
8 Going Forward
Takeaways
What I learned:
Working with that many variables can be hard in terms of the finding related ones. Coming up with a concrete problem statement at the very beginning of the analysis helped me to stay on track.
Said that, a good domain-knowledge is essential for every single data-related research.
No matter how sure you (and your colleagues) would be about one particular outcome, the data may (and most probably will) show something else and more.
Next Steps
If I’d have more time, I could study the followings:
❶ Finding identical (or similar) car models and examine a single varying variable. For instance, to check such cars with a tow bar and without. However, finding too many similar cars would be difficult.
❷ Investigating the effect of the color. People’s choices for the new and second hand car could be interesting to study.
❸ Performing other studies with different data models and ML techniques.
Browse my projects by category:
ALL • Data • UX • Arch


