When our dataset includes categorical variables, we need to preprocess them before making some calculations or visualizing relationships, for instance, in a correlation matrix.
In most cases, we’d encode the categorical variables into numerical values. I did write about some of them before but they require a deeper understanding and also there are many more encoding techniques. Here I’ll examine only some of the most commonly used ones:
- Label Encoding
Converts categories into integer codes. - Ordinal Encoding
Converts categorical data with an inherent order into integer labels. - One-Hot Encoding
Converts categorical variables into binary columns, each representing one category. - Target Encoding
Encodes categories based on the mean of the target variable. - Frequency Encoding
Encodes categories based on their frequency in the dataset. - Binary Encoding
Converts categories into binary format.
It is a little hard to grasp them at once, since they are highly related to each other. The main ideas are similar, but their differences come from the needs of the analysis and the form & size of the dataset.
That’s why it was more helpful to me to start with the two and continue building up from there. Those two are Label Encoding and Ordinal Encoding; they look quite similar and it is easy to mix up with each other.
1. Label Encoding
Assigns arbitrary integer values to categories without any consideration of order.
Example:
[“apple”, “banana”, “cherry”] → [0, 1, 2]
Use Case:
- When the categories are nominal (no inherent order).
- Works well with algorithms that treat the values as labels rather than ordinal (e.g., tree-based algorithms like decision trees or random forests).
- Pitfall: Algorithms like linear regression might interpret the numbers as ordinal, leading to misleading results.
2. Ordinal Encoding
Assigns integers based on a predefined order that reflects the natural ranking of the categories.
Example:
[“low”, “medium”, “high”] → [0, 1, 2]
Use Case:
- When the categories are ordinal and there is an inherent hierarchy or ranking among them.
- The encoding reflects this order, making it meaningful for algorithms that interpret numerical relationships.
What is the difference: Label vs. Ordinal
When we check both outputs, it looks like there is no difference between these two methods. The key difference is that ordinal encoding intentionally reflects a meaningful order, while label encoding creates an unintended one.
Key Differences:
| Aspect | Label Encoding | Ordinal Encoding |
| Assignment of Numbers | Arbitrary | Reflects category order |
| Use for Nominal Data | Yes | No |
| Use for Ordinal Data | Rarely | Yes |
| Semantic Meaning | No inherent meaning in order | Encodes meaningful ranking |
Key Problem with Label Encoding for Nominal Data
Label encoding introduces numerical values that can imply a false order to nominal categories, which can confuse algorithms that assume numerical relationships. This is especially problematic for:
- Linear models (e.g., regression or logistic regression): These treat the encoded values as numerical, implying order and distance.
- Clustering algorithms (e.g., k-means): These use Euclidean distance, which can lead to spurious results if the numerical encoding is arbitrary.
When Label Encoding Works
Despite its pitfalls, label encoding is not inherently flawed, it works well in specific contexts:
- Tree-based algorithms: Algorithms like decision trees, random forests, and gradient boosting (e.g., XGBoost, LightGBM) do not assume numerical relationships between features. They split data based on categories directly, so label encoding is safe for nominal data in these cases.
- Quick preprocessing: Label encoding can be a simple and quick way to preprocess data when exploratory analysis or lightweight models are the goal.
Alternative Solutions for Nominal Data
To avoid introducing false order, other encoding methods (like the below ones) are often better suited for nominal data.
3. One-Hot Encoding:
Each category is represented as a binary column.
Example:
[“apple”, “banana”, “cherry”] →
apple banana cherry
1 0 0
0 1 0
0 0 1
- Advantages: Prevents false order by treating all categories as equally distant.
- Disadvantages: The dimensionality is increasing.
4. Target Encoding (in supervised learning):
Replaces each category with a statistic (e.g., mean of the target variable for that category or other aggregate for each category).
Example:
Category: [“A”, “B”, “A”, “C”, “B”, “C”, “A”]
Target (numeric): [100, 200, 150, 300, 250, 350, 175]
Encoded feature becomes: [141.67, 225.00, 141.67, 325.00, 225.00, 325.00, 141.67]
Advantages:
- Reduces the dimensionality compared to one-hot encoding.
- Captures the relationship between the categorical variable and the target variable.
- Useful for high-cardinality categorical features (features with many unique categories).
- Can be used with algorithms that don’t natively handle categorical data, like linear regression or neural networks.
Disadvantages:
- Can lead to data leakage if not done carefully. Data leakage occurs when information from the test set influences the training process.
- Sensitive to outliers in the target variable.
Avoiding Data Leakage
To prevent data leakage, the target mean for each category must be computed only from the training data available at the time. Typically, this is done using techniques like:
- K-Fold Mean Encoding: Compute the mean within each fold during cross-validation.
- Leave-One-Out Encoding: Exclude the current row’s target value when computing the mean for that category.
- Smoothing: Combine the category mean with the overall target mean to reduce the effect of small sample sizes or outliers.
5. Frequency Encoding:
Replaces each category with its frequency in the dataset.
Example:
[“apple”, “apple”, “banana”, “cherry”] →
[0.5, 0.5, 0.25, 0.25]
Advantages:
- Encodes categories into a single column, reducing dimensionality compared to one-hot encoding.
- Useful for datasets with high cardinality (many unique categories).
- The frequency of occurrence often carries meaningful information, especially in imbalanced datasets. (suitable for tree-based models)
- Easy to implement and computationally efficient, requiring just a count and mapping operation.
Disadvantages:
- Implies that categories with higher frequencies are more significant, which may not always align with the underlying data distribution or context.
- Reduces interpretability since the original categories are replaced by numerical values.
- Models might overfit to the specific frequency values if they are highly correlated with the target, especially in small datasets.
- Linear models may interpret frequency values as numerical magnitudes rather than categorical indicators, leading to misleading relationships.
When to use:
- Best for high-cardinality categorical variables in tree-based models or when frequency itself is meaningful (e.g., popularity, ranking).
- Avoid for linear models or datasets where frequency doesn’t represent an inherent relationship with the target.
6. Binary Encoding
Combines the ideas of one-hot encoding and ordinal encoding but is more memory-efficient.
Each category is first assigned a unique integer (as in label encoding), and then the integers are converted to binary. Each binary digit becomes a separate column.
Example:
Categories: [“A”, “B”, “C”, “D”]
Label Encoding: [0, 1, 2, 3]
Binary Representation:
0 → 0 0
1 → 0 1
2 → 1 0
3 → 1 1
The encoded matrix:
Col1 Col2
0 0
0 1
1 0
1 1
- Advantages: Reduces dimensionality compared to one-hot encoding.
- Disadvantages: May not perform well for nominal variables in some algorithms.
Comparing the Encoding Methods
As seen above, the most commonly used encoding techniques primarily differ in terms of dimensionality and whether they account for the importance of order in the categorical data.
Key Dimensions for Comparison:
- Dimensionality: How many new features or columns are created by the encoding process.
- Order Sensitivity: Whether the encoding method preserves or imposes an order among categories.
- Information Preservation: How well the method retains information about the categories’ relationships.
- Interpretability: Whether the encoded values are easy to interpret in terms of the original data.
| Encoding Method | Dimensionality | Preserves / Imposes Order | Use Case |
| Label Encoding | Low (one column) | Yes (imposes order unintentionally for nominal data) | Works with tree-based models; avoid for nominal data with non-order-sensitive algorithms. |
| Ordinal Encoding | Low (one column) | Yes (imposes order) | For ordinal data where order matters (e.g., “low”, “medium”, “high”). |
| One-Hot Encoding | High (one column per category) | No | For nominal data, avoids false order and works with most models. |
| Target Encoding | Low (one column) | No (depends on target distribution) | Captures relationship with target; good for high-cardinality features. |
| Frequency Encoding | Low (one column) | No | Simplifies high-cardinality features; retains category prevalence. |
| Binary Encoding | Moderate (log₂ of categories) | No | Reduces dimensionality while preserving category information. |
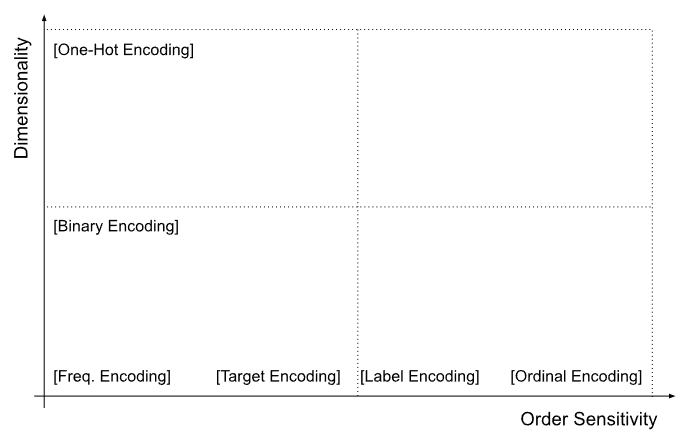
Summary lists like the one above are helpful but sometimes I need a visual to get a better sense. Let’s plot a graph, where x-axis would be order sensitivity and y-axis would be dimensionality. In such a graph, the placements of above mentioned encoding techniques would be:
Quadrant 1 (Top-Left: High Dimensionality, No Order Sensitivity):
- One-Hot Encoding: High dimensionality because it creates one column per category. Completely ignores order.
Quadrant 2 (Top-Right: High Dimensionality, High Order Sensitivity):
- Rare or Inapplicable: High dimensionality is uncommon for order-sensitive methods, as ordinal data is usually compactly encoded.
Quadrant 3 (Bottom-Left: Low Dimensionality, No Order Sensitivity):
- Frequency Encoding: Low dimensionality with no order sensitivity; captures prevalence of categories.
- Binary Encoding: Reduces dimensionality while maintaining nominal information.
- Target Encoding: Low dimensionality with order-agnostic nature, depending on target variable distribution.
Quadrant 4 (Bottom-Right: Low Dimensionality, High Order Sensitivity):
- Ordinal Encoding: Assigns numbers based on a known order.
- Label Encoding: Implicitly imposes order (although unintentionally for nominal data).
Advanced Encoding Methods
There are other encoding methods like:
- Hash Encoding (Feature Hashing)
- BaseN Encoding
- Leave-One-Out Encoding
- Count Encoding
- Weighted Target Encoding
- Probability Ratio Encoding
- Embedding Encoding
And many more advanced ones are:
- Polynomial Coding (Helmert Encoding)
- Contrast Encoding (Deviation Coding)
- Weight of Evidence (WoE) Encoding
- CatBoost Encoding
- James-Stein Encoding
- Gaussian Encoding
- Entity Embeddings
- Ordinal Encoding with Thresholding
- Cluster-Based Encoding
- Ordinal Logistic Regression Encoding
- Principal Component Encoding (PCA Encoding)
I listed them just for my future reference, I won’t study them now. But a quick summary of some less common methods could be:
| Encoding Method | Use Case | Key Benefit |
| Polynomial Coding | Statistical modeling | Captures group-level contrasts |
| Weight of Evidence (WoE) | Credit scoring, binary targets | Log odds for binary target |
| CatBoost Encoding | Gradient boosting with CatBoost | Reduces data leakage |
| Gaussian Encoding | Avoiding overfitting in small datasets | Adds noise to target encoding |
| Entity Embeddings | Complex relationships in large datasets | Dense, continuous representations |
| Cluster-Based Encoding | Grouping similar categories | Simplifies complex categories |
Sticking to the more commonly used techniques, such as one-hot encoding, target encoding, or ordinal encoding, is often sufficient for most applications.
