The statistical significance is the claim that the results of a test or experiment are not explainable by chance alone. A hypothesis test can help us determine whether our observed data is statistically significant, or likely due to chance.
There are two different types of hypothesis tests: one-sample and two-sample. A one-sample test determines whether or not a population parameter, like a mean or proportion, is equal to a specific value.
A two-sample test determines whether or not two population parameters, such as two means or two proportions, are equal to each other.
One-sample Test
A data professional might conduct a one-sample hypothesis test to determine if:
- A company’s average sales revenue is equal to a target value.
- A medical treatment’s average rate of success is equal to a set goal.
- A stock portfolio’s average rate of return is equal to a market benchmark.
The one-sample z-test makes the following assumptions:
- The data is a random sample of a normally-distributed population.
- The population standard deviation is known.
Let’s explore an example to get a better understanding of the role of statistical significance in hypothesis testing.
Example: Mean battery life
Let’s review the steps for conducting a hypothesis test:
- State the null hypothesis and the alternative hypothesis.
- Choose a significance level.
- Find the p-value.
- Reject or fail to reject the null hypothesis.
Imagine we’re a data professional working for a computer company. The company claims the mean battery life for their best selling laptop is 8.5 hours with a standard deviation of 0.5 hours. Recently, the engineering team redesigned the laptop to increase the battery life. The team takes a random sample of 40 redesigned laptops. The sample mean is 8.7 hours.
The team asks us to determine if the increase in mean battery life is statistically significant, or if it’s due to random chance. We decided to conduct a z-test to find out.
Step 1: State the null hypothesis and alternative hypothesis
The null hypothesis typically assumes that our observed data occurs by chance, and it is not statistically significant. In this case, our null hypothesis says that there is no actual effect on mean battery life in the population of laptops.
The alternative hypothesis typically assumes that our observed data does not occur by chance, and is statistically significant. In this case, our alternative hypothesis says that there is an effect on mean battery life in the population of laptops.
In this example, we formulate the following hypotheses:
- H0: μ = 8.5 (the mean battery life of all redesigned laptops is equal to 8.5 hours)
- Ha: μ > 8.5 (the mean battery life of all redesigned laptops is greater than 8.5 hours)
Step 2: Choose a significance level
The significance level, or alpha (α), is the threshold at which we will consider a result statistically significant. The significance level is also the probability of rejecting the null hypothesis when it is true.
Typically, data professionals set the significance level at 0.05, or 5%. That means results at least as extreme as ours only have a 5% chance (or less) of occurring when the null hypothesis is true.
Note: 5% is a conventional choice, and not a magical number. It’s based on tradition in statistical research and education. Other common choices are 1% and 10%. We can adjust the significance level to meet the specific requirements of our analysis. A lower significance level means an effect has to be larger to be considered statistically significant.
Another note: As a best practice, we should set a significance level before we begin our test. Otherwise, we might end up in a situation where we are manipulating the results to suit our convenience.
In this example, we choose a significance level of 5%, which is the company’s standard for research.
Step 3: Find the p-value
P-value refers to the probability of observing a difference in our results as or more extreme than the difference observed when the null hypothesis is true.
Our p-value helps us determine whether a result is statistically significant. A low p-value indicates high statistical significance, while a high p-value indicates low or no statistical significance.
Every hypothesis-test features:
- A test statistic that indicates how closely our data match the null hypothesis. For a z-test, our test statistic is a z-score; for a t-test, it’s a t-score.
- A corresponding p-value that tells us the probability of obtaining a result at least as extreme as the observed result if the null hypothesis is true.
As a data professional, we’ll almost always calculate p-value on our computer, using a programming language like Python or other statistical software. However, let’s briefly explore the concepts involved in the calculation to get a better understanding of how it works.
The p-value is calculated from what’s called a test statistic. In hypothesis testing, the test statistic is a value that shows how closely our observed data matches the distribution expected under the null hypothesis.
So if we assume the null hypothesis is true and the mean battery life is equal to 8.5 hours, the data for battery life follows a normal distribution. The test statistic shows where our observed data, a sample mean battery life of 8.5 hours, will fall on that distribution.
Since we’re conducting a z-test, our test statistic is a z-score. Recall that a z-score is a measure of how many standard deviations below or above the population mean a data point is. Z-scores tell us where our values lie on a normal distribution. The following formula gives us a test statistic z, based on our sample data.
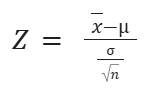
Where x-bar is the sample mean, mu is the population mean, sigma is the population standard deviation, and n is the sample size.
In our example we’re conducting a z-test, so our test statistic is a z-score of 2.53. Based on this test statistic, we calculate a p-value of 0.0057, or 0.57%.
Step 4: Reject or fail to reject the null hypothesis
In a hypothesis test, we compare our p-value to your significance level to decide whether our results are statistically significant.
There are two main rules for drawing a conclusion about a hypothesis test:
- If our p-value is less than our significance level, we reject the null hypothesis.
- If our p-value is greater than our significance level, we fail to reject the null hypothesis.
Note: Data professionals and statisticians always say “fail to reject” rather than “accept.” This is because hypothesis tests are based on probability, not certainty: acceptance implies certainty. In general, data professionals avoid claiming certainty about results based on statistical methods.
In this example, our p-value of 0.57% is less than our significance level of 5%. Our test provides sufficient evidence to conclude that the mean battery life of all redesigned laptops has increased from 8.5 hours. We reject the null hypothesis. We determine that our results are statistically significant.
Two-sample Test: Means
As a reminder: There are two different types of hypothesis tests: one-sample and two-sample. A one-sample test determines whether or not a population parameter, like a mean or proportion, is equal to a specific value.
A two-sample test determines whether or not two population parameters, such as two means or two proportions, are equal to each other. In data analytics, two-sample tests are frequently used for A/B testing.
The two-sample t-test for means makes the following assumptions:
- The two samples are independent of each other.
- For each sample, the data is drawn randomly from a normally distributed population.
- The population standard deviation is unknown.
Typically, data professionals use a z-test when the population standard deviation is known, and use a t-test when the population standard deviation is unknown and needs to be estimated from the data. In practice, the population standard deviation is usually unknown because it’s difficult to get complete data on large populations. So data professionals use the t-test for practical applications.
While the test statistic for a z-test is a Z-score, the test statistic for a t-test is a T-score. And while Z-scores are based on the standard normal distribution, T-scores are based on the t-distribution.
The graph of the t-distribution has a bell shape that is similar to the standard normal distribution, but the t-distribution has bigger tails than the standard normal distribution does. The bigger tails indicate the higher frequency of outliers that come with small datasets.
As the sample size increases, the t-distribution approaches the normal distribution. For a t-test, the test statistic follows a t-distribution under the null hypothesis.
One-tailed and two-tailed tests
A one-tailed test results when the alternative hypothesis states that the actual value of a population parameter is either less than or greater than the value in the null hypothesis. A one-tailed test may be either left-tailed or right-tailed.
A two-tailed test results when the alternative hypothesis states that the actual value of the parameter does not equal the value in the null hypothesis.
For example, imagine a test in which the null hypothesis states that the mean weight of a penguin population equals 30 lbs.
- In a left-tailed test, the alternative hypothesis might state that the mean weight of the penguin population is less than (“<“) 30 lbs.
- In a right-tailed test, the alternative hypothesis might state that the mean weight of the penguin population is greater than (“>”) 30 lbs.
- In a two-tailed test, the alternative hypothesis might state that the mean weight of the penguin population is not equal (“≠”) to 30 lbs.
Example: One-tailed tests
Imagine we’re a data professional working for an online retail company. The company claims that at least 80% of its customers are satisfied with their shopping experience. We survey a random sample of 100 customers. According to the survey, 73% of customers say they are satisfied. Based on the survey data, you conduct a z-test to evaluate the claim that at least 80% of customers are satisfied.
Let’s review the steps for conducting a hypothesis test:
- State the null hypothesis and the alternative hypothesis.
- Choose a significance level.
- Find the p-value.
- Reject or fail to reject the null hypothesis.
First, we state the null and alternative hypotheses:
- H0: P >= 0.80 (the proportion of satisfied customers is greater than or equal to 80%)
- Ha: P < 0.80 (the proportion of satisfied customers is less than 80%)
Next, we choose a significance level of 0.05, or 5%.
Then, we calculate our p-value based on our test statistic. P-value is the probability of observing results as or more extreme than those observed when the null hypothesis is true. In the context of hypothesis testing, “extreme” means extreme in the direction(s) of the alternative hypothesis.
Our test statistic is a z-score of 1.75 and our p-value is 0.04.
Since this is a left-tailed test, the p-value is the probability that the z-score is less than 1.75 standard units away from the mean to the left. In other words, it’s the probability that the z-score is less than -1.75.
The probability of getting a value less than our z-score of -1.75 is calculated by taking the area under the distribution curve to the left of the z-score. The area under this part of the curve is the same as our p-value: 0.04.
Finally, we draw a conclusion. Since our p-value of 0.04 is less than your significance level of 0.05, we reject the null hypothesis.
Note: In a different testing scenario, our test statistic might be positive 1.75, and we might be interested in values as great or greater than the z-score 1.75. In that case, our p-value would be located on the right tail of the distribution, and we’d be conducting a right-tailed test.
Example: Two-tailed tests
Now, imagine our previous example has a slightly different set up. Suppose the company claims that 80% of its customers are satisfied with their shopping experience. To test this claim, we survey a random sample of 100 customers. According to the survey, 73% of customers say they are satisfied. Based on the survey data, we conduct a z-test to evaluate the claim that 80% of customers are satisfied.
First, we state the null and alternative hypotheses:
- H0: P = 0.80 (the proportion of satisfied customers equals 80%)
- Ha: P ≠ 0.80 (the proportion of satisfied customers does not equal 80%)
Next, we choose a significance level of 0.05, or 5%.
Then, we calculate our p-value based on our test statistic. Our test statistic is a z-score of 1.75. Since this is a two-tailed test, the p-value is the probability that the z-score is less than -1.75 or greater than 1.75.
In a two-tailed test, our p-value corresponds to the area under the curve on both the left tail and right tail of the distribution. So, in this case, our p-value = 0.04 + 0.04 = 0.08.
Finally, we draw a conclusion. Since our p-value of 0.08 is greater than our significance level of 0.05, we fail to reject the null hypothesis.
Two-sample tests: Proportions
A data professional might use a two-sample z-test to compare the proportion of
- defects among manufacturing products on two assembly lines,
- side effects to a new medicine for two trial groups,
- support for a new law among registered voters in two districts.
Disclaimer: Like most of my posts, this content is intended solely for educational purposes and was created primarily for my personal reference. At times, I may rephrase original texts, and in some cases, I include materials such as graphs, equations, and datasets directly from their original sources.
I typically reference a variety of sources and update my posts whenever new or related information becomes available. For this particular post, the primary source was Google Advanced Data Analytics Professional Certificate.
