Introduction
In a previous activity, we analyzed a subset of data that contained information about the NBA players and their performance records. We conducted feature engineering to determine which features would most effectively predict a player’s career duration. We will now use those insights to build a model that predicts whether a player will have an NBA career lasting five years or more.
The data for this activity consists of performance statistics from each player’s rookie year. There are 1,341 observations, and each observation in the data represents a different player in the NBA. Your target variable is a Boolean value that indicates whether a given player will last in the league for five years. Since you previously performed feature engineering on this data, it is now ready for modeling.
Step 1: Imports
# Import relevant libraries and modules.
import pandas as pd
from sklearn import naive_bayes
from sklearn import model_selection
from sklearn import metrics# Load extracted_nba_players_data.csv into a DataFrame called extracted_data
extracted_data = pd.read_csv('extracted_nba_players_data.csv')# Display the first 10 rows of data
extracted_data.head(10)| fg | 3p | ft | reb | ast | stl | blk | tov | target_5yrs | total_points | efficiency | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 34.7 | 25.0 | 69.9 | 4.1 | 1.9 | 0.4 | 0.4 | 1.3 | 0 | 266.4 | 0.270073 |
| 1 | 29.6 | 23.5 | 76.5 | 2.4 | 3.7 | 1.1 | 0.5 | 1.6 | 0 | 252.0 | 0.267658 |
| 2 | 42.2 | 24.4 | 67.0 | 2.2 | 1.0 | 0.5 | 0.3 | 1.0 | 0 | 384.8 | 0.339869 |
| 3 | 42.6 | 22.6 | 68.9 | 1.9 | 0.8 | 0.6 | 0.1 | 1.0 | 1 | 330.6 | 0.491379 |
| 4 | 52.4 | 0.0 | 67.4 | 2.5 | 0.3 | 0.3 | 0.4 | 0.8 | 1 | 216.0 | 0.391304 |
| 5 | 42.3 | 32.5 | 73.2 | 0.8 | 1.8 | 0.4 | 0.0 | 0.7 | 0 | 277.5 | 0.324561 |
| 6 | 43.5 | 50.0 | 81.1 | 2.0 | 0.6 | 0.2 | 0.1 | 0.7 | 1 | 409.2 | 0.605505 |
| 7 | 41.5 | 30.0 | 87.5 | 1.7 | 0.2 | 0.2 | 0.1 | 0.7 | 1 | 273.6 | 0.553398 |
| 8 | 39.2 | 23.3 | 71.4 | 0.8 | 2.3 | 0.3 | 0.0 | 1.1 | 0 | 156.0 | 0.242424 |
| 9 | 38.3 | 21.4 | 67.8 | 1.1 | 0.3 | 0.2 | 0.0 | 0.7 | 0 | 155.4 | 0.435294 |
Step 2: Model preparation
# Define the y (target) variable
y = extracted_data['target_5yrs']
# Define the X (predictor) variables
X = extracted_data.drop('target_5yrs', axis = 1)Display the first 10 rows of our target and predictor variables. This will help us get a sense of how the data is structured.
# Display the first 10 rows of your target data
y.head(10)0 0 1 0 2 0 3 1 4 1 5 0 6 1 7 1 8 0 9 0 Name: target_5yrs, dtype: int64
Given that the target variable contains both 1 and 0 indicates that it is binary and requires a model suitable for binary classification.
# Display the first 10 rows of your predictor variables
X.head(10)| fg | 3p | ft | reb | ast | stl | blk | tov | total_points | efficiency | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 34.7 | 25.0 | 69.9 | 4.1 | 1.9 | 0.4 | 0.4 | 1.3 | 266.4 | 0.270073 |
| 1 | 29.6 | 23.5 | 76.5 | 2.4 | 3.7 | 1.1 | 0.5 | 1.6 | 252.0 | 0.267658 |
| 2 | 42.2 | 24.4 | 67.0 | 2.2 | 1.0 | 0.5 | 0.3 | 1.0 | 384.8 | 0.339869 |
| 3 | 42.6 | 22.6 | 68.9 | 1.9 | 0.8 | 0.6 | 0.1 | 1.0 | 330.6 | 0.491379 |
| 4 | 52.4 | 0.0 | 67.4 | 2.5 | 0.3 | 0.3 | 0.4 | 0.8 | 216.0 | 0.391304 |
| 5 | 42.3 | 32.5 | 73.2 | 0.8 | 1.8 | 0.4 | 0.0 | 0.7 | 277.5 | 0.324561 |
| 6 | 43.5 | 50.0 | 81.1 | 2.0 | 0.6 | 0.2 | 0.1 | 0.7 | 409.2 | 0.605505 |
| 7 | 41.5 | 30.0 | 87.5 | 1.7 | 0.2 | 0.2 | 0.1 | 0.7 | 273.6 | 0.553398 |
| 8 | 39.2 | 23.3 | 71.4 | 0.8 | 2.3 | 0.3 | 0.0 | 1.1 | 156.0 | 0.242424 |
| 9 | 38.3 | 21.4 | 67.8 | 1.1 | 0.3 | 0.2 | 0.0 | 0.7 | 155.4 | 0.435294 |
The data indicates that all of the predictor variables are continuous numerical values, so it is important that the model selected is suitable for continuous features.
Perform a split operation
# Perform the split operation on data
X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y, test_size=0.25, random_state=0)# Print the shape (rows, columns) of the output from the train-test split
# Print the shape of X_train
print(X_train.shape)
# Print the shape of X_test
print(X_test.shape)
# Print the shape of y_train
print(y_train.shape)
# Print the shape of y_test
print(y_test.shape)(1005, 10)
(335, 10)
(1005,)
(335,)
Step 3: Model building
Using the assumption that our features are normally distributed and continuous, the Gaussian Naive Bayes algorithm is most appropriate for our data. While our data may not perfectly adhere to these assumptions, this model will still yield the most usable and accurate results.
# Assign `nb` to be the appropriate implementation of Naive Bayes
nb = naive_bayes.GaussianNB()
# Fit the model on your training data
nb.fit(X_train, y_train)
# Apply your model to predict on your test data. Call this "y_pred"
y_pred = nb.predict(X_test)Step 4: Results and evaluation
# Print your accuracy score
print('accuracy score:'), print(metrics.accuracy_score(y_test, y_pred))
# Print your precision score
print('precision score:'), print(metrics.precision_score(y_test, y_pred))
# Print your recall score
print('recall score:'), print(metrics.recall_score(y_test, y_pred))
# Print your f1 score
print('f1 score:'), print(metrics.f1_score(y_test, y_pred))accuracy score:
0.6895522388059702
precision score:
0.8405797101449275
recall score:
0.5858585858585859
f1 score:
0.6904761904761905
In classification problems, accuracy is useful to know but may not be the best metric by which to evaluate this model. While accuracy is often the most intuitive metric, it is a poor evaluation metric in some cases. In particular, if we have imbalanced classes, a model could appear accurate but be poor at balancing false positives and false negatives.
Precision and recall scores are both useful to evaluate the correct predictive capability of a model because they balance the false positives and false negatives inherent in prediction.
The F1 score balances the precision and recall performance to give a combined assessment of how well this model delivers predictions. In this case, the F1 score is 0.6905, which suggests reasonable predictive power in this model.
Gain clarity with the confusion matrix
# Construct the confusion matrix for your predicted and test values
cm = metrics.confusion_matrix(y_test, y_pred)
# Create the display for your confusion matrix
disp = metrics.ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=nb.classes_)
# Plot the visual in-line
disp.plot()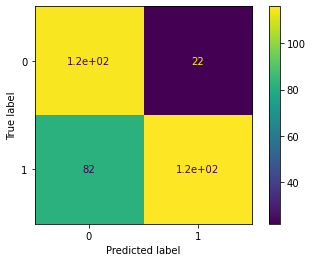
Considerations
How would we present our results to your team?
- Showcase the data used to create the prediction and the performance of the model overall.
- Review the sample output of the features and the confusion matrix to indicate the model’s performance.
- Highlight the metric values, emphasizing the F1 score.
How would we summarize our findings to stakeholders?
- The model created provides some value in predicting an NBA player’s chances of playing for five years or more.
- Notably, the model performed better at predicting true positives than it did at predicting true negatives. In other words, it more accurately identified those players who will likely play for more than five years than it did those who likely will not.
Disclaimer: Like most of my posts, this content is intended solely for educational purposes and was created primarily for my personal reference. At times, I may rephrase original texts, and in some cases, I include materials such as graphs, equations, and datasets directly from their original sources.
I typically reference a variety of sources and update my posts whenever new or related information becomes available. For this particular post, the primary source was Google Advanced Data Analytics Professional Certificate program.
