So far we’ve discussed how to apply PACE to logistic regression.
- We’ve analyzed our data by understanding the model assumptions to the best of our ability, ensuring we have a binary outcome variable.
- We’ve constructed our model and created several evaluation metrics.
- Now we can begin executing and sharing the results.
Interpreting a logistic regression model involves examining coefficients and computing metrics. After we fit our logistic regression model to training data, we can access the coefficient estimates from the model using code in Python. We can then use those values to understand how the model makes predictions.
Here we’ll check an example of how to interpret coefficients from a logistic regression model, as well as things to consider when choosing metrics for model evaluation.
Coefficients from the model
To understand how a logistic regression model works, it is important to start with the equation that describes the relationship between the variables. That equation is also called the logit function.
The logit function
When the logit function is written in terms of the independent variables, it conveys the following: there is a linear relationship between each independent variable, X, and the logit of the probability that the dependent variable, Y, equals 1. The logit of that probability is the logarithm of the odds of that probability.
The equation for the logit function in binomial logistic regression is shown below. This involves the probability that Y equals 1, because 1 is the typical outcome of interest in binary classification, where the possible values of Y are 1 and 0.
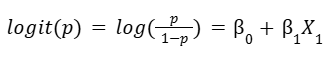
where p = P(Y=1)
Interpret coefficients
Imagine we have built a binomial logistic regression model for predicting emails as spam or non-spam. The dependent variable, Y, is whether an email is spam (1) or non-spam (0). The independent variable, X1, is the message length. Assume that clf is the classifier we fitted to training data.
We can use the following code to access the coefficient β1 estimated by the model: clf.coef_
If the estimated β1 is 0.186, for example, that means a one-unit increase in message length is associated with a 0.186 increase in the log odds of p. To interpret change in odds of Y as a percentage, we can exponentiate β1, as follows.
eβ1 = e0.186 ≈ 1.204
So, for every one-unit increase in message length, we can expect that the odds the email is spam increases by 1.204, or 20.4%.
Things to consider when choosing metrics
The next important step after examining the coefficients from a logistic regression model is evaluating the model through metrics. The most commonly used metrics include precision, recall, and accuracy. The following sections describe things to keep in mind when choosing between these.
When to use precision
Using precision as an evaluation metric is especially helpful in contexts where the cost of a false positive is quite high and much higher than the cost of a false negative.
For example, in the context of email spam detection, a false positive (predicting a non-spam email as spam) would be more costly than a false negative (predicting a spam email as non-spam). A non-spam email that is misclassified could contain important information, such as project status updates from a vendor to a client or assignment deadline announcements from an instructor to a class of students.
When to use recall
Using recall as an evaluation metric is especially helpful in contexts where the cost of a false negative is quite high and much higher than the cost of a false positive.
For example, in the context of fraud detection among credit card transactions, a false negative (predicting a fraudulent credit card charge as non-fraudulent) would be more costly than a false positive (predicting a non-fraudulent credit card charge as fraudulent). A fraudulent credit card charge that is misclassified could lead to the customer losing money, undetected.
When to use accuracy
It is helpful to use accuracy as an evaluation metric when we specifically want to know how much of the data at hand has been correctly categorized by the classifier.
Accuracy is an appropriate metric to use when the data is balanced, in other words, when the data has a roughly equal number of positive examples and negative examples. Otherwise, accuracy can be biased.
For example, imagine that 95% of a dataset contains positive examples, and the remaining 5% contains negative examples. Then we train a logistic regression classifier on this data and use this classifier predict on this data. If we get an accuracy of 95%, that does not necessarily indicate that this classifier is effective. Since there is a much larger proportion of positive examples than negative examples, the classifier may be biased towards the majority class (positive) and thus the accuracy metric in this context may not be meaningful.
When the data we are working with is imbalanced, we consider either transforming it to be balanced or using a different evaluation metric other than accuracy.
A sample to interpret the results of a logistic regression
Let’s bring our previous data sample about activities.
To recap, we wanted to understand how changes in vertical acceleration are related to whether a person is lying down or not. Our focus now is on what the Beta coefficient means in our equation.
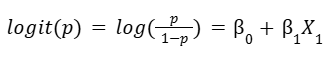
In this case, a one-unit increase in vertical acceleration is associated with a β1 (unit) increase in the log odds of p. But if we exponentiate the log odds, then we can determine how much the odds change as a percentage based on changes in vertical acceleration.
So, e to the power of β1 (eβ1) is how many times the odds of p will increase or decrease for every one-unit increase in vertical acceleration.
We calculated before our coefficient as negative 0.118. Now we can exponentiate the coefficient:
β1 = -0.118
eβ1 = e-0.118 = 0.89
We can say that for every one unit increase in vertical acceleration, we expect that the odds the person is lying down decreases by 11 percent. This makes sense because if someone is moving faster in a vertical direction, they are probably not lying down.
Given that we have found a strong predictor of whether a person is lying down or not, we can consider the larger picture. For example, classifying motion can help detect falls or suspicions of injury. Our strong predictor can be a piece of a larger story about providing care to older adults.
When the coefficient is positive
Next, let’s examine how the interpretation would change in different scenarios.
Let’s try an example where the coefficient is positive. Imagine the coefficient is 0.25. Then we exponentiate and get e^0.25, which is 1.28, rounded to the nearest hundredth.
β1 = 0.25
eβ1 = e0.25 = 1.28
Then we could say that for every one unit increase in X, we expect the odds of y being one to increase by 28%.
When there are multiple independent variables
Now imagine there are other factors in the model, such as acceleration in other directions. When there are multiple independent variables in a logistic regression model, just like in a linear regression model, we have to report coefficients while holding other variables constant.
So we could say for every one unit increase in X, holding other variables constant, we expect the odds of y being one to increase by 28%.
Reporting the uncertainty
Moving beyond the coefficient, it is always helpful to state the P-value and confidence interval to give additional information about how likely the result is just by chance. Scikit-learn does not have a built-in way of getting p-values or confidence intervals, but statsmodels does. (This is a great example of how different tools and packages can give us different information.)
When presenting the results, it can be helpful to include a confusion matrix and some statistics on precision, recall, accuracy or ROC, AUC. However, depending on the situation, we might want to include all of them or focus on a subset of metrics.
Which metrics to choose
Consider that certain industries or organizations may have preferred metrics given how they manage their modeling process. It’s important to check with our team about this.
Take for example, the case of detecting spam texts (or unsolicited messages) sent to many recipients. Only a small fraction of text messages that we receive are probably spam. But if our goal is to accurately classify spam text messages so we don’t give away private information or click on a bad link, then we’re really only focusing on how well we can detect spam messages. In fact, in this case, accuracy is not a good metric.
Let’s say only 3% of text messages are spam. That means 97% are text messages we want to receive from friends and family or automated messages from service providers. So if a model predicts that 100% of messages are not spam, that model would have a 97% accuracy rate, which seems great.
But it’s not that good in this context because the model will not have detected any spam at all, even though 3% of messages are in fact spam.
In the case of spam messages, recall is probably a more meaningful metric. Recall will tell us the proportion of spam messages that the model was actually able to detect.
Precision, on the other hand, would tell us the proportion of data points labeled spam, that were actually spam. Precision essentially measures the quality of our spam labeling.
There are other metrics that we can explore as well, such as AIC and BIC, which can help determine how good a model is while factoring in how complex the model is. So there is no one solution that works every time. We always have to contextualize the data, the problem, and the available solutions.
Disclaimer: Like most of my posts, this content is intended solely for educational purposes and was created primarily for my personal reference. At times, I may rephrase original texts, and in some cases, I include materials such as graphs, equations, and datasets directly from their original sources.
I typically reference a variety of sources and update my posts whenever new or related information becomes available. For this particular post, the primary source was Google Advanced Data Analytics Professional Certificate.
