Introduction
Accuracy, precision, recall and F1 score are top metrics in classification techniques and they are especially useful for measuring unbalanced classes.
When building any model intended for production, it’s essential to improve the results. We might change specific parameters to discover how the performance improves. We should always keep in mind that model-building is an inherently iterative process. The first model that we produce will almost never be the one that gets deployed.
After tweaking the parameters or changing how features are engineered in each model, the performance metrics provide a basis for comparing the models to each other and against themselves.
Evaluation metrics for classification models
Metrics like R2, mean squared error (MSE), root mean squared error (RMSE), and mean absolute error (MAE) are all useful when evaluating the error of a prediction on a continuous variable.
Classification models, on the other hand, predict a class and cannot be evaluated using the same metrics as linear regression models. With a linear regression model, our model predicts a continuous value that has a unit label (e.g., dollars, kilograms, minutes, etc.) and our evaluation pertains to the residuals of the model’s predictions—the difference between predicted and actual values:
But with a binary logistic regression, our observations are represented by two classes; they are either one value or another. The model predicts a probability, and assigns observations to a class based on that probability:
Evaluation metrics like accuracy, precision, and recall can all be derived from a confusion matrix, which is a graphical representation of our model.
Accuracy
Accuracy is the proportion of data points that are correctly classified. It is an overall representation of model performance.
Accuracy = (true positives + true negatives) / total predictions
Accuracy is often unsuitable to use when there is a class imbalance in the data, because it’s possible for a model to have high accuracy by predicting the majority class every time. In such a case, the model would score well, but it may not be a useful model.
Precision
Precision measures the proportion of positive predictions that are true positives.
Precision = true positives / (true positives + false positives)
Precision is a good metric to use when it’s important to avoid false positives. For example, if our model is designed to initially screen out ineligible loan applicants before a human review, then it’s best to err on the side of caution and not automatically disqualify people before a person can review the case more carefully.
Recall
Recall measures the proportion of actual positives that are correctly classified.
Recall= true positives / (true positives + false negatives)
Recall is a good metric to use when it’s important that we identify as many true responders as possible. For example, if our model is identifying poisonous mushrooms, it’s better to identify all of the true occurrences of poisonous mushrooms, even if that means making a few more false positive predictions.
Precision-recall curves
A precision-recall curve is a way to visualize the performance of a classifier at different decision thresholds (a.k.a. classification thresholds). In the context of binary classification, a decision threshold is a probability cutoff for differentiating the positive class from the negative class. In most modeling libraries, including scikit-learn, the default decision threshold is 0.5 (i.e., if a sample’s predicted probability of response is ≥ 0.5, then it’s labeled “positive”).
In a precision-recall curve, necessarily, as one metric increases, the other generally decreases, and vice versa. For example, suppose our model’s decision threshold is very high: 0.98. Our model will not predict a positive class unless it’s at least 98% sure. Our precision will therefore be very high—our model’s predicted positives will likely all be true positives. But the model will probably catch very few actual positives because it’s too strict, so the recall will be very low.
The same is true for the inverse. If our model casts a very wide net and predicts many positives, it will likely capture many true positives, but it will also mistakenly label many negative samples as positive. Thus, the model might have a perfect recall but a very poor precision. The art and the science is to find a model that maximizes both metrics and best suits our use case.
ROC curves
Receiver operating characteristic (ROC) curves are similar to precision-recall curves in that they visualize the performance of a classifier at different decision thresholds. However, this curve is a plot of the true positive rate against the false positive rate.
True Positive Rate: Equivalent/synonymous to recall
True positive rate = true positives / (true positives + false negatives)
False Positive Rate: The ratio between the false positives and the total count of observations that should be predicted as False.
False positive rate = false positives / (false positives + true negatives)
For each point on an ROC curve, the horizontal and vertical coordinates represent the false positive rate and the true positive rate at the corresponding threshold.
An ideal model perfectly separates all negatives from all positives, and gives all real positive cases a very high probability and all real negative cases a very low probability. In other words, on the graph above, it would be in the upper-left-most corner. It would have a perfect TP rate (1) and a perfect FP rate (0).
To contrast, imagine starting from a decision threshold just above zero: 0.001. In this case, it’s likely that all real positives would be captured and there would be very few, if any, false negatives, because for a model to label a sample “negative,” its predicted probability must be < 0.001. The true positive rate would be ≈ 1, which is excellent, but its false positive rate would also be ≈ 1, which is very bad. This decision threshold would result in TP/FP rates that would be at the upper-right-most area of the graph above.
To reiterate: Graphically, the closer our model’s TP/FP rate is to the top-left corner of the plot, the better the model is at classifying the data. Also note that by default most modeling libraries use a decision threshold of 0.5 to separate positive predictions and negative predictions. However, there are some cases where 0.5 might not be the optimal decision threshold to use.
AUC
AUC is a measure of the two-dimensional area underneath an ROC curve. AUC provides an aggregate measure of performance across all possible classification thresholds. One way to interpret AUC is to consider it as the probability that the model ranks a random positive sample more highly than a random negative sample. AUC ranges in value from 0.0 to 1.0. In the following example, the AUC is the shaded region below the dotted curve.
F1 score
F1 score is a measurement that combines both precision and recall into a single expression, giving each equal importance. It is calculated as:
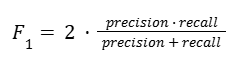
This combination is known as the harmonic mean. F1 score can range [0, 1], with zero being the worst and one being the best. The idea behind this metric is that it penalizes low values of either metric, which prevents one very strong factor (precision or recall) from “carrying” the other, when it is weaker.
The following figure illustrates a comparison of the F1 score to the mean of precision and recall. In each case, precision is held constant while recall ranges from 0 to 1.
The F1 score never exceeds the mean. In fact, it is only equal to the mean in a single case: when precision equals recall. The more one score diverges from the other, the more F1 score penalizes. Note that we could swap precision and recall values in this experiment and the scores would be the same.
Plotting the means and F1 scores for all values of precision against all values of recall results in two planes.
While the coordinate plane of the mean is flat, the plane of the F1 score is pulled further downward the more one score diverges from the other. This penalizing effect makes F1 score a useful measurement of model performance.
F𝛽 score
If we still want to capture both precision and recall in a single metric, but we consider one more important than the other, we can use F𝛽 score (pronounced F-beta). In an F𝛽 score, 𝛽 is a factor that represents how many times more important recall is compared to precision.
In the case of F1 score, 𝛽 = 1, and recall is therefore 1x as important as precision (i.e., they are equally important). However, an F2 score has 𝛽 = 2, which means recall is twice as important as precision; and if precision is twice as important as recall, then 𝛽 = 0.5. The formula for F𝛽 score is:
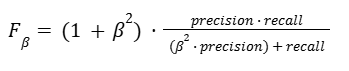
Disclaimer: Like most of my posts, this content is intended solely for educational purposes and was created primarily for my personal reference. At times, I may rephrase original texts, and in some cases, I include materials such as graphs, equations, and datasets directly from their original sources.
I typically reference a variety of sources and update my posts whenever new or related information becomes available. For this particular post, the primary source was Google Advanced Data Analytics Professional Certificate program.
