In previous examples, we plotted points in two dimensional space, where it was clear if the model was correctly assigning points to clusters. We also were able to visualize the data in three dimensions. Unfortunately, most cases data professionals encounter on the job are not so easy. Our data will have many more than three dimensions, so we will not be able to visualize how each observation relates to those around it. We might not even know how many clusters there should be.
So how do we decide the value for K? And once we do, how do we know if our model is working as intended?
In linear and logistic regression, we used metrics such as R squared, mean squared error, area under the ROC curve, precision, and recall to evaluate the effectiveness of our model. But in unsupervised learning, we don’t have any labeled data to compare our model against. The metrics aren’t applicable. In fact, our model isn’t predicting anything. Instead, it’s grouping observations based on their similarities. It’s up to us to investigate and understand the different clusters.
But if we have some domain knowledge or the problem we’re trying to solve has its own constraints, we can use these things to our advantage. For example, maybe we’re investigating customer segmentation for a service that offers four different subscription levels, then we’d probably want to use four as our value for K.
What makes for a good clustering model
Before we get started with evaluation metrics, let’s consider what makes for a good clustering model. Basically, we want clearly identifiable clusters. This means that within each cluster or intracluster, the points are close to each other. It also means that between the clusters themselves or intercluster, we want lots of empty space.
One way to evaluate the intracluster space in a K-means model is to identify its inertia. This is a different concept from inertia as it’s defined in physics. Here, inertia is defined as the sum of the squared distances between each observation and its nearest centroid.
Essentially, this is a measurement of how closely related observations are to other observations within the same cluster. That information is then aggregated across all the clusters to produce a single score for the particular metric being measured.
Another important metric for evaluating our K-means model is the silhouette score. This is a more precise evaluation metric than inertia because it also takes into account the separation between clusters. Silhouette score is defined as the mean of the silhouette coefficients of all the observations in the model.
The silhouette score helps evaluate our model, provides insight as to what the optimal value for K should be, and uses both intracluster and intercluster measurements in its calculation.
Inertia and silhouette coefficient metrics
In a good clustering model, ideally we’d have tight clusters of closely-related observations. Each cluster is well separated from other clusters.
Inertia
Inertia is a measurement of intracluster distance. It indicates how compact the clusters are in a model. It is the sum of the squared distances between each observation and its closest centroid. It’s a measurement of intra-cluster distance. So it gauges how closely related each observation is to the other observations in its own cluster. Inertia can be represented by this formula:
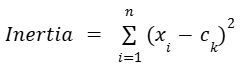
where
n is the total number of observations in the data,
xi is the location of a particular observation,
ck is the centroid of the cluster that the observation xi is in.
The more compact the clusters, the lower the inertia, because there’s less distance between each observation and its nearest centroid. Therefore, it’s important for inertia to be as close to zero as possible.
Note, however, that inertia only measures intracluster distance. Therefore, both of the clusterings in the figure below have the same inertia.
Can inertia ever be zero?
Well, it’s possible, but this scenario wouldn’t offer any new insight into the data. Here’s why: In one case, if all observations were identical, this would mean all data points are in the same location, then inertia equals zero for all values of k. The second case is when the number of clusters is equal to the number of observations. If each observation is in its own cluster, then its centroid is itself.
Evaluating inertia
Inertia is a useful metric to determine how well our clustering model identifies meaningful patterns in the data. But it’s generally not very useful by itself. If our model has an inertia of 53.25, is that good? It depends.
The measurement becomes meaningful when it’s compared to the inertia values and k values of other models on the same data. As we increase the number of clusters (k), the inertia value will drop, but there comes a point where adding more clusters will have only small changes in inertia. And it’s this transition that we need to detect.
The elbow method
Inertia is a great metric because it helps us to decide on the optimal k value. We do this by using the elbow method. In the elbow method, we first build models with different values of k. Then we plot the inertia for each k value. Here’s an example.
This plot compares the inertias of nine different K-means models, one for each value of k from 2 through 10. It’s clear that inertia begins very high when the data is grouped into two clusters. The three-cluster model, however, has much lower inertia, creating a steep negative slope between two and three clusters. After that, the rate of inertial decline slows down dramatically, as indicated by the much flatter line in the plot.
Notice that the greater the value is for k, the lower the inertia. But this doesn’t mean that we should always select high k values. A low inertia is great, but if it results in meaningless or inexplicable clusters, it doesn’t help us at all. If we add more and more clusters with only minimal improvement to inertia, we’re only adding complexity without capturing real structure in the data.
A good way of choosing an optimal k value is to find the elbow of the curve. This is the value of k at which the decrease in inertia starts to level off. In this example, that occurs when we use three clusters. However sometimes it might be difficult to choose between two consecutive values of k. In that case, it’s up to us to determine which is best for our particular project.
In the case above, it seems that the elbow occurs at the three-cluster model, but there’s still a considerable decline in inertia from three to four clusters. There’s not necessarily a “correct” answer. It might be worth doing some analysis on the cluster assignments of both models to check for ourselves which is more meaningful.
Silhouette score
Silhouette score is defined as the mean of the silhouette coefficients of all the observations in the model. Each observation has its own silhouette coefficient which is calculated as:
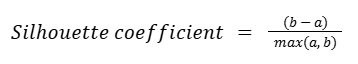
where
a is the mean distance from that observation to all other observations in the same cluster,
b is the mean distance from that observation to each observation in the next closest cluster.
The silhouette coefficient can be anywhere between negative 1 and 1.
-1 ≤ s ≤ 1
If an observation has a silhouette coefficient close to one, it means that it’s both nicely within its own cluster and well separated from other clusters.
A value of zero indicates that the observation is on the boundary between clusters.
If our observation has a silhouette coefficient close to negative 1, it may be in the wrong cluster.
When using silhouette score to help determine how many clusters our model should have, we’ll generally want to opt for the k value that maximizes our silhouette score.
Note that, unlike inertia, silhouette coefficients contain information about both intracluster distance (captured by the variable a) and intercluster distance (captured by the variable b). In the figure below, the points in the three clusters on the left have lower silhouette coefficients than the points in the three on the right.
As with inertia values, we can plot silhouette scores for different models to compare them against each other.
In this example, it’s evident that a three-cluster model has a higher silhouette score than any other model. This indicates that this model results in individual clusters that are tighter and more separated from other clusters, more so than any other model tried. Based on this diagram, the data is probably best grouped into three clusters.
Key takeaways
Inertia and silhouette score are useful metrics to help determine how meaningful our model’s cluster assignments are. Both are especially helpful when our data has too many dimensions (features) to visualize in 2-D or 3-D space.
Inertia:
- Measures intracluster distance.
- Equal to the sum of the squared distance between each point and the centroid of the cluster that it’s assigned to.
- Used in elbow plots.
- All else equal, lower values are generally better.
Silhouette score:
- Measures both intercluster distance and intracluster distance.
- Equal to the average of all points’ silhouette coefficients.
- Can be between -1 and +1 (greater values are better).
Disclaimer: Like most of my posts, this content is intended solely for educational purposes and was created primarily for my personal reference. At times, I may rephrase original texts, and in some cases, I include materials such as graphs, equations, and datasets directly from their original sources.
I typically reference a variety of sources and update my posts whenever new or related information becomes available. For this particular post, the primary source was Google Advanced Data Analytics Professional Certificate program.
