Modeling objective
The modeling objective is to build and test a Naive Bayes model that uses banking data to predict whether a customer will churn. If a customer churns, it means they left the bank and took their business elsewhere. If we can predict customers who are likely to churn, we can take measures to retain them before they do. These measures could be promotions, discounts, or other incentives to boost customer satisfaction and, therefore, retention.
Target variable
Remember, our target variable is called Exited. This is a Boolean value that indicates whether or not a customer left the bank (0 = did not leave, 1 = did leave). For each customer, our model will predict whether they should have a 0 or a 1 in the Exited column.
Important Note on Model design
This is a classification task, because we are trying to predict on a binary class. Naive Bayes often works well for this kind of task. However, recall that there are several different implementations of the Naive Bayes algorithm in scikit-learn, and each assumes that all of our predictor variables are of a single type (e.g., Gaussian for continuous variables, Bernoulli for binary variables, etc.).
Our data has all different types of predictor variables! The real-world data is never perfect. Sometimes the data breaks the assumptions of our model. In practice, we’ll have to do the best we can with what we have.
In this case, if we wanted to build the best possible Naive Bayes model, we’d treat each variable according to their different types and distributions, and then combine each conditional probability to get the final prediction for each observation. That’s advanced data science, and beyond the scope of this post.
Here, we’re going to use the GaussianNB classifier. This implementation assumes that all of your variables are continuous and that they have a Gaussian (i.e., normal) distribution. Our data doesn’t perfectly adhere to these assumptions, but a Gaussian model may still yield usable results, even with imperfect data.
Import libraries and read data
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import recall_score, precision_score, f1_score, accuracy_score
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplayWe’re going to use the prepared dataframe that we made in a previous post. Remember, we:
- Dropped the
RowNumber,CustomerId,Surname, andGendercolumns - Dummy encoded the
Geographycolumn to convert categorical to Boolean - Engineered a new feature called
Loyalty, by dividing each customer’s tenure by their age
churn_df = pd.read_csv('churn_df.csv')
churn_df.head()| CreditScore | Age | Tenure | Balance | NumOfProducts | HasCrCard | IsActiveMember | EstimatedSalary | Exited | Loyalty | Geography_Germany | Geography_Spain | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 619 | 42 | 2 | 0.00 | 1 | 1 | 1 | 101348.88 | 1 | 0.047619 | 0 | 0 |
| 1 | 608 | 41 | 1 | 83807.86 | 1 | 0 | 1 | 112542.58 | 0 | 0.024390 | 0 | 1 |
| 2 | 502 | 42 | 8 | 159660.80 | 3 | 1 | 0 | 113931.57 | 1 | 0.190476 | 0 | 0 |
| 3 | 699 | 39 | 1 | 0.00 | 2 | 0 | 0 | 93826.63 | 0 | 0.025641 | 0 | 0 |
| 4 | 850 | 43 | 2 | 125510.82 | 1 | 1 | 1 | 79084.10 | 0 | 0.046512 | 0 | 1 |
Check the class balance
# Check class balance
churn_df['Exited'].value_counts()0 7963 1 2037 Name: Exited, dtype: int64
The class is split roughly 80/20. In other words, ~20% of the people in this dataset churned. This is an unbalanced dataset, but it’s not extreme.
Also, remember that the Naive Bayes formula depends on class priors (P(c)) to make predictions. Because of this, performing class balancing (e.g., upsampling or downsampling) would change those terms in a way that would no longer reflect the real-world distribution of the data.
For these reasons, we’ll proceed without altering the class balance of our target variable.
Drop dependent variables
Remember that Naive Bayes models operate best when there’s conditional independence between the predictor variables. When we prepared our data, we engineered a feature called Loyalty by dividing Tenure by Age. Because this new feature is just the quotient of two existing variables, it’s no longer conditionally independent. Therefore, we’ll drop Tenure and Age to help adhere to the assumptions of our model.
# Drop Tenure and Age variables
churn_df = churn_df.drop(['Tenure', 'Age'], axis=1)
churn_df.head()| CreditScore | Balance | NumOfProducts | HasCrCard | IsActiveMember | EstimatedSalary | Exited | Loyalty | Geography_Germany | Geography_Spain | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 619 | 0.00 | 1 | 1 | 1 | 101348.88 | 1 | 0.047619 | 0 | 0 |
| 1 | 608 | 83807.86 | 1 | 0 | 1 | 112542.58 | 0 | 0.024390 | 0 | 1 |
| 2 | 502 | 159660.80 | 3 | 1 | 0 | 113931.57 | 1 | 0.190476 | 0 | 0 |
| 3 | 699 | 0.00 | 2 | 0 | 0 | 93826.63 | 0 | 0.025641 | 0 | 0 |
| 4 | 850 | 125510.82 | 1 | 1 | 1 | 79084.10 | 0 | 0.046512 | 0 | 1 |
Split the data
Below we include the argument stratify=y. If our master data has a class split of 80/20, stratifying ensures that this proportion is maintained in both the training and test data. =y tells the function that it should use the class ratio found in the y variable (our target).
The less data we have overall, and the greater our class imbalance, the more important it is to stratify when we split the data. If we didn’t stratify, then the function would split the data randomly, and we could get an unlucky split that doesn’t get any of the minority class in the test data, which means we wouldn’t be able to effectively evaluate our model.
# Define the y (target) variable
y = churn_df['Exited']
# Define the X (predictor) variables
X = churn_df.copy()
X = X.drop('Exited', axis=1)
# Split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, \
stratify=y, random_state=42)Modeling
1. Unscaled data
# Fit the model
gnb = GaussianNB()
gnb.fit(X_train, y_train)
# Get the predictions on test data
y_preds = gnb.predict(X_test)Now we can check how our model performs using the evaluation metrics we imported.
print('Accuracy:', '%.3f' % accuracy_score(y_test, y_preds))
print('Precision:', '%.3f' % precision_score(y_test, y_preds))
print('Recall:', '%.3f' % recall_score(y_test, y_preds))
print('F1 Score:', '%.3f' % f1_score(y_test, y_preds))Accuracy: 0.796
Precision: 0.000
Recall: 0.000
F1 Score: 0.000
This isn’t very good. Our precision, recall, and F1 scores are all zero. What’s going on? Let’s consider our precision formula:
precision = true positives / (false positives + true positives)
There are two ways for the model to have a precision of zero. The first is if the numerator is zero, which would mean that our model didn’t predict any true positives.
The second is if the denominator is also zero, which would mean that our model didn’t predict any positives at all. Dividing by zero results in an undefined value, but scikit-learn will return a value of zero in this case. Depending on our modeling environment, we may get a warning that tells us there’s a denominator of zero.
We don’t have a warning, so let’s check which situation is occurring here. If we call np.unique() on the model’s predictions and it doesn’t return an array containing [0, 1], we’ll know it’s not predicticting any churned customers.
# Check unique values in predictions
np.unique(y_preds)array([0])
This confirms that the model predicted 0 (not churned) for every sample in the test data.
Consider why this might be. Perhaps we did something wrong in our modeling process, or maybe using GaussianNB on predictor variables of different types and distributions just doesn’t make a good model. Maybe there were problems with the data.
Before we give up, maybe the data can give us some insight into what might be happening or what further steps we can take. Let’s use describe() to inspect the X data.
# Get descriptive stats for data
X.describe()| CreditScore | Balance | NumOfProducts | HasCrCard | IsActiveMember | EstimatedSalary | Loyalty | Geography_Germany | Geography_Spain | |
|---|---|---|---|---|---|---|---|---|---|
| count | 10000.000000 | 10000.000000 | 10000.000000 | 10000.00000 | 10000.000000 | 10000.000000 | 10000.000000 | 10000.000000 | 10000.000000 |
| mean | 650.528800 | 76485.889288 | 1.530200 | 0.70550 | 0.515100 | 100090.239881 | 0.137936 | 0.250900 | 0.247700 |
| std | 96.653299 | 62397.405202 | 0.581654 | 0.45584 | 0.499797 | 57510.492818 | 0.089506 | 0.433553 | 0.431698 |
| min | 350.000000 | 0.000000 | 1.000000 | 0.00000 | 0.000000 | 11.580000 | 0.000000 | 0.000000 | 0.000000 |
| 25% | 584.000000 | 0.000000 | 1.000000 | 0.00000 | 0.000000 | 51002.110000 | 0.064516 | 0.000000 | 0.000000 |
| 50% | 652.000000 | 97198.540000 | 1.000000 | 1.00000 | 1.000000 | 100193.915000 | 0.129032 | 0.000000 | 0.000000 |
| 75% | 718.000000 | 127644.240000 | 2.000000 | 1.00000 | 1.000000 | 149388.247500 | 0.200000 | 1.000000 | 0.000000 |
| max | 850.000000 | 250898.090000 | 4.000000 | 1.00000 | 1.000000 | 199992.480000 | 0.555556 | 1.000000 | 1.000000 |
Something that stands out is that the Loyalty variable we created is on a vastly different scale than some of the other variables we have, such as Balance or EstimatedSalary. The maximum value of Loyalty is 0.56, while the maximum for Balance is over 250,000—almost six orders of magnitude greater!
2. Scaled data
One thing that we can usually try when modeling is scaling our predictor variables. Some models require us to scale the data in order for them to operate as expected, others don’t. Naive Bayes does not require data scaling. However, sometimes packages and libraries need to make assumptions and approximations in their calculations. We’re already breaking some of these assumptions by using the GaussianNB classifier on this dataset, and it may not be helping that some of our predictor variables are on very different scales. In general, scaling might not improve the model, but it probably won’t make it worse. Let’s try scaling our data.
We’ll use a function called MinMaxScaler, that normalizes each column so every value falls in the range of [0, 1]. The column’s maximum value would scale to 1, and its minimum value would scale to 0. Everything else would fall somewhere between. This is the formula:
xscaled = (x − xmin) / (xmax − xmin)
To use a scaler, we must fit it to the training data, and transform both the training data and the test data using that same scaler.
# Import the scaler function
from sklearn.preprocessing import MinMaxScaler
# Instantiate the scaler
scaler = MinMaxScaler()
# Fit the scaler to the training data
scaler.fit(X_train)
# Scale the training data
X_train = scaler.transform(X_train)
# Scale the test data
X_test = scaler.transform(X_test)Now we’ll repeat the steps to fit our model, only this time we’ll fit it to our new scaled data.
# Fit the model
gnb_scaled = GaussianNB()
gnb_scaled.fit(X_train, y_train)
# Get the predictions on test data
scaled_preds = gnb_scaled.predict(X_test)print('Accuracy:', '%.3f' % accuracy_score(y_test, scaled_preds))
print('Precision:', '%.3f' % precision_score(y_test,scaled_preds))
print('Recall:', '%.3f' % recall_score(y_test, scaled_preds))
print('F1 Score:', '%.3f' % f1_score(y_test, scaled_preds))Accuracy: 0.806
Precision: 0.544
Recall: 0.303
F1 Score: 0.389
It works now! The model is far from perfect, but at least it’s predicting churned customers now.
Evaluation
Let’s examine more closely how our model classified the test data. We’ll do this with a confusion matrix. Here’s a helper function that will allow us to plot a confusion matrix for our model.
def conf_matrix_plot(model, x_data, y_data):
'''
Accepts as argument model object, X data (test or validate), and y data (test or validate).
Return a plot of confusion matrix for predictions on y data.
'''
model_pred = model.predict(x_data)
cm = confusion_matrix(y_data, model_pred, labels=model.classes_)
disp = ConfusionMatrixDisplay(confusion_matrix=cm,
display_labels=model.classes_,
)
disp.plot(values_format='') # to suppress scientific notation
plt.show()conf_matrix_plot(gnb_scaled, X_test, y_test)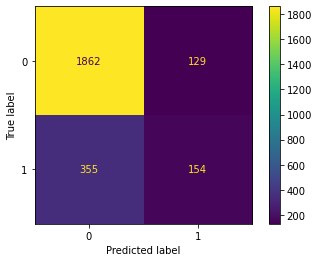
All of our model metrics can be derived from the confusion matrix, and each metric tells its own part of the story. What stands out most in the confusion matrix is that the model misses a lot of customers who will churn. In other words, there are a lot of false negatives. 355, to be exact. This is why our recall score is only 0.303.
Would we use this model? It depends. For one thing, we’d certainly want to develop other models to see if they perform better.
Disclaimer: Like most of my posts, this content is intended solely for educational purposes and was created primarily for my personal reference. At times, I may rephrase original texts, and in some cases, I include materials such as graphs, equations, and datasets directly from their original sources.
I typically reference a variety of sources and update my posts whenever new or related information becomes available. For this particular post, the primary source was Google Advanced Data Analytics Professional Certificate program.
