Introduction
Here we’ll assume, we work as a consultant for an airline. The airline is interested in knowing if a better in-flight entertainment experience leads to higher customer satisfaction. They would like us to construct and evaluate a model that predicts whether a future customer would be satisfied with their services given previous customer feedback about their flight experience.
The data for this activity is for a sample size of 129,880 customers. It includes data points such as class, flight distance, and in-flight entertainment, among others. Our goal will be to utilize a binomial logistic regression model to help the airline model and better understand this data.
Imports & Load
# Standard operational package imports
import numpy as np
import pandas as pd
# Important imports for preprocessing, modeling, and evaluation
from sklearn.preprocessing import OneHotEncoder
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
import sklearn.metrics as metrics
# Visualization package imports
import matplotlib.pyplot as plt
import seaborn as snsdf_original = pd.read_csv("Invistico_Airline.csv")
df_original.head(n = 10)| satisfaction | Customer Type | Age | Type of Travel | Class | Flight Distance | Seat comfort | Departure/Arrival time convenient | Food and drink | Gate location | … | Online support | Ease of Online booking | On-board service | Leg room service | Baggage handling | Checkin service | Cleanliness | Online boarding | Departure Delay in Minutes | Arrival Delay in Minutes | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | satisfied | Loyal Customer | 65 | Personal Travel | Eco | 265 | 0 | 0 | 0 | 2 | … | 2 | 3 | 3 | 0 | 3 | 5 | 3 | 2 | 0 | 0.0 |
| 1 | satisfied | Loyal Customer | 47 | Personal Travel | Business | 2464 | 0 | 0 | 0 | 3 | … | 2 | 3 | 4 | 4 | 4 | 2 | 3 | 2 | 310 | 305.0 |
| 2 | satisfied | Loyal Customer | 15 | Personal Travel | Eco | 2138 | 0 | 0 | 0 | 3 | … | 2 | 2 | 3 | 3 | 4 | 4 | 4 | 2 | 0 | 0.0 |
| 3 | satisfied | Loyal Customer | 60 | Personal Travel | Eco | 623 | 0 | 0 | 0 | 3 | … | 3 | 1 | 1 | 0 | 1 | 4 | 1 | 3 | 0 | 0.0 |
| 4 | satisfied | Loyal Customer | 70 | Personal Travel | Eco | 354 | 0 | 0 | 0 | 3 | … | 4 | 2 | 2 | 0 | 2 | 4 | 2 | 5 | 0 | 0.0 |
| 5 | satisfied | Loyal Customer | 30 | Personal Travel | Eco | 1894 | 0 | 0 | 0 | 3 | … | 2 | 2 | 5 | 4 | 5 | 5 | 4 | 2 | 0 | 0.0 |
| 6 | satisfied | Loyal Customer | 66 | Personal Travel | Eco | 227 | 0 | 0 | 0 | 3 | … | 5 | 5 | 5 | 0 | 5 | 5 | 5 | 3 | 17 | 15.0 |
| 7 | satisfied | Loyal Customer | 10 | Personal Travel | Eco | 1812 | 0 | 0 | 0 | 3 | … | 2 | 2 | 3 | 3 | 4 | 5 | 4 | 2 | 0 | 0.0 |
| 8 | satisfied | Loyal Customer | 56 | Personal Travel | Business | 73 | 0 | 0 | 0 | 3 | … | 5 | 4 | 4 | 0 | 1 | 5 | 4 | 4 | 0 | 0.0 |
| 9 | satisfied | Loyal Customer | 22 | Personal Travel | Eco | 1556 | 0 | 0 | 0 | 3 | … | 2 | 2 | 2 | 4 | 5 | 3 | 4 | 2 | 30 | 26.0 |
10 rows × 22 columns
Data exploration, data cleaning, and model preparation
Remember that logistic regression models expect numeric data.
df_original.dtypessatisfaction object Customer Type object Age int64 Type of Travel object Class object Flight Distance int64 Seat comfort int64 Departure/Arrival time convenient int64 Food and drink int64 Gate location int64 Inflight wifi service int64 Inflight entertainment int64 Online support int64 Ease of Online booking int64 On-board service int64 Leg room service int64 Baggage handling int64 Checkin service int64 Cleanliness int64 Online boarding int64 Departure Delay in Minutes int64 Arrival Delay in Minutes float64 dtype: object
df_original['satisfaction'].value_counts(dropna = False)satisfied 71087 dissatisfied 58793 Name: satisfaction, dtype: int64
54.7 percent (71,087/129,880) of customers were satisfied. While this is a simple calculation, this value can be compared to a logistic regression model’s accuracy.
Check for missing values
An assumption of logistic regression models is that there are no missing values.
df_original.isnull().sum()Out[6]:
satisfaction 0 Customer Type 0 Age 0 Type of Travel 0 Class 0 Flight Distance 0 Seat comfort 0 Departure/Arrival time convenient 0 Food and drink 0 Gate location 0 Inflight wifi service 0 Inflight entertainment 0 Online support 0 Ease of Online booking 0 On-board service 0 Leg room service 0 Baggage handling 0 Checkin service 0 Cleanliness 0 Online boarding 0 Departure Delay in Minutes 0 Arrival Delay in Minutes 393 dtype: int64
For this activity, the airline is specifically interested in knowing if a better in-flight entertainment experience leads to higher customer satisfaction. The Arrival Delay in Minutes column won’t be included in the binomial logistic regression model; however, the airline might become interested in this column in the future.
For now, the missing values should be removed for two reasons:
- There are only 393 missing values out of the total of 129,880, so these are a small percentage of the total.
- This column might impact the relationship between entertainment and satisfaction.
df_subset = df_original.dropna(axis=0).reset_index(drop = True)Prepare the data
If we want to create a plot (sns.regplot) of our model to visualize results later in the notebook, the independent variable Inflight entertainment cannot be “of type int” and the dependent variable satisfaction cannot be “of type object.”
df_subset = df_subset.astype({"Inflight entertainment": float})# Convert the categorical column satisfaction into numeric through one-hot encoding
df_subset['satisfaction'] = OneHotEncoder(drop='first').fit_transform(df_subset[['satisfaction']]).toarray()To examine what one-hot encoding did to the DataFrame, let’s output the first 10 rows of df_subset.
df_subset.head(10)| satisfaction | Customer Type | Age | Type of Travel | Class | Flight Distance | Seat comfort | Departure/Arrival time convenient | Food and drink | Gate location | … | Online support | Ease of Online booking | On-board service | Leg room service | Baggage handling | Checkin service | Cleanliness | Online boarding | Departure Delay in Minutes | Arrival Delay in Minutes | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.0 | Loyal Customer | 65 | Personal Travel | Eco | 265 | 0 | 0 | 0 | 2 | … | 2 | 3 | 3 | 0 | 3 | 5 | 3 | 2 | 0 | 0.0 |
| 1 | 1.0 | Loyal Customer | 47 | Personal Travel | Business | 2464 | 0 | 0 | 0 | 3 | … | 2 | 3 | 4 | 4 | 4 | 2 | 3 | 2 | 310 | 305.0 |
| 2 | 1.0 | Loyal Customer | 15 | Personal Travel | Eco | 2138 | 0 | 0 | 0 | 3 | … | 2 | 2 | 3 | 3 | 4 | 4 | 4 | 2 | 0 | 0.0 |
| 3 | 1.0 | Loyal Customer | 60 | Personal Travel | Eco | 623 | 0 | 0 | 0 | 3 | … | 3 | 1 | 1 | 0 | 1 | 4 | 1 | 3 | 0 | 0.0 |
| 4 | 1.0 | Loyal Customer | 70 | Personal Travel | Eco | 354 | 0 | 0 | 0 | 3 | … | 4 | 2 | 2 | 0 | 2 | 4 | 2 | 5 | 0 | 0.0 |
| 5 | 1.0 | Loyal Customer | 30 | Personal Travel | Eco | 1894 | 0 | 0 | 0 | 3 | … | 2 | 2 | 5 | 4 | 5 | 5 | 4 | 2 | 0 | 0.0 |
| 6 | 1.0 | Loyal Customer | 66 | Personal Travel | Eco | 227 | 0 | 0 | 0 | 3 | … | 5 | 5 | 5 | 0 | 5 | 5 | 5 | 3 | 17 | 15.0 |
| 7 | 1.0 | Loyal Customer | 10 | Personal Travel | Eco | 1812 | 0 | 0 | 0 | 3 | … | 2 | 2 | 3 | 3 | 4 | 5 | 4 | 2 | 0 | 0.0 |
| 8 | 1.0 | Loyal Customer | 56 | Personal Travel | Business | 73 | 0 | 0 | 0 | 3 | … | 5 | 4 | 4 | 0 | 1 | 5 | 4 | 4 | 0 | 0.0 |
| 9 | 1.0 | Loyal Customer | 22 | Personal Travel | Eco | 1556 | 0 | 0 | 0 | 3 | … | 2 | 2 | 2 | 4 | 5 | 3 | 4 | 2 | 30 | 26.0 |
10 rows × 22 columns
Create the training and testing data
X = df_subset[["Inflight entertainment"]]
y = df_subset["satisfaction"]
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.3, random_state=42) Other variables, like Departure Delay in Minutes seem like they can be potentially influential to customer satisfaction. This is why only using one independent variable might not be ideal.
Model building
clf = LogisticRegression().fit(X_train,y_train)clf.coef_array([[0.99751462]])
clf.intercept_array([-3.19355406])
sns.regplot(x="Inflight entertainment", y="satisfaction", data=df_subset, logistic=True, ci=None)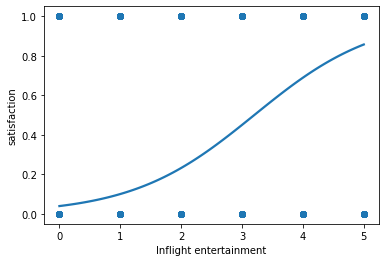
The graph seems to indicate that the higher the inflight entertainment value, the higher the customer satisfaction, though this is currently not the most informative plot. The graph currently doesn’t provide much insight into the data points, as Inflight entertainment is categorical.
Results and evaluation
Now that we’ve completed our regression, let’s review and analyze our results. We’ll input the holdout dataset into the predict function to get the predicted labels from the model and save these predictions as a variable called y_pred.
# Save predictions.
y_pred = clf.predict(X_test)print(y_pred)[1. 0. 0. ... 0. 0. 0.]
# Use predict_proba to output a probability
clf.predict_proba(X_test)array([[0.14258068, 0.85741932],
[0.55008402, 0.44991598],
[0.89989329, 0.10010671],
...,
[0.89989329, 0.10010671],
[0.76826225, 0.23173775],
[0.55008402, 0.44991598]])
# Use predict to output 0's and 1's
clf.predict(X_test)array([1., 0., 0., ..., 0., 0., 0.])
Analyze the results
print("Accuracy:", "%.6f" % metrics.accuracy_score(y_test, y_pred))
print("Precision:", "%.6f" % metrics.precision_score(y_test, y_pred))
print("Recall:", "%.6f" % metrics.recall_score(y_test, y_pred))
print("F1 Score:", "%.6f" % metrics.f1_score(y_test, y_pred))Accuracy: 0.801529
Precision: 0.816142
Recall: 0.821530
F1 Score: 0.818827
Produce a confusion matrix
Data professionals often like to know the types of errors made by an algorithm. To obtain this information, we’ll produce a confusion matrix.
cm = metrics.confusion_matrix(y_test, y_pred, labels = clf.classes_)
disp = metrics.ConfusionMatrixDisplay(confusion_matrix = cm,display_labels = clf.classes_)
disp.plot()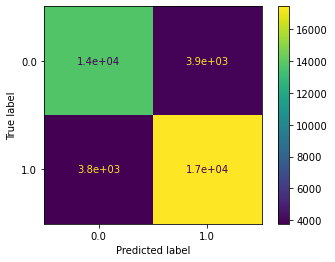
- Two of the quadrants are under 4,000, which are relatively low numbers. These numbers relate to false positives and false negatives. Additionally, the other two quadrants—the true positives and true negatives—are both high numbers above 13,000.
- There isn’t a large difference in the number of false positives and false negatives.
- Using more than a single independent variable in the model training process could improve model performance. This is because other variables, like
Departure Delay in Minutes,seem like they could potentially influence customer satisfaction.
Considerations
What could we recommend to stakeholders?
- Customers who rated in-flight entertainment highly were more likely to be satisfied. Improving in-flight entertainment should lead to better customer satisfaction.
- The model is 80.2 percent accurate. This is an improvement over the dataset’s customer satisfaction rate of 54.7 percent.
- The success of the model suggests that the airline should invest more in model development to examine if adding more independent variables leads to better results. Building this model could not only be useful in predicting whether or not a customer would be satisfied but also lead to a better understanding of what independent variables lead to happier customers.
Disclaimer: Like most of my posts, this content is intended solely for educational purposes and was created primarily for my personal reference. At times, I may rephrase original texts, and in some cases, I include materials such as graphs, equations, and datasets directly from their original sources.
I typically reference a variety of sources and update my posts whenever new or related information becomes available. For this particular post, the primary source was Google Advanced Data Analytics Professional Certificate.
