Probability is the branch of mathematics that deals with measuring and quantifying uncertainty.
Types of Probability
A. Objective probability
Based on statistics, experiment, and mathematical measurements. There are two types of objective probability:
Classical probability is based on formal reasoning about events with equally likely outcomes. To calculate classical probability for an event, we divide the number of desired outcomes by the total number of possible outcomes. (like flipping a coin, or drawing a card from a deck)
While classical probability applies to events with equally likely outcomes, data professionals use empirical probability to describe more complex events.
Empirical probability is based on experimental or historical data; it represents the likelihood of an event occurring based on the previous results of an experiment or past events. To calculate empirical probability, we divide the number of times a specific event occurs by the total number of events. (the probability that a person prefers strawberry ice cream)
Data professionals rely on empirical probability to help them make accurate predictions based on sample data.
B. Subjective probability
Based on personal feelings, experience, or judgment.
It’s important to know the difference between subjective and objective probability when we evaluate a prediction or make a decision.
The principles of probability
The probability that an event will occur is expressed as a number between 0 and 1. There are lots of possibilities in between 0 and 1.
Random experiment – (aka statistical experiment) a process whose outcome cannot be predicted with certainty. All random experiments have three things in common.
- The experiment can have more than one possible outcome,
- we can represent each possible outcome in advance,
- and the outcome of the experiment depends on chance.
To calculate the probability of a random experiment, we divide the number of desired outcomes by the total number of possible outcomes. (classical probability)
# of desired outcomes ÷ total # of possible outcomes
In statistics, the result of a random experiment is called an outcome. For example, if we roll a die, there are six possible outcomes: 1, 2, 3, 4, 5, 6.
An event is a set of one or more outcomes. Using the example of rolling a die, an event might be rolling an even number. The event of rolling an even number consists of the outcomes 2, 4, 6. Or, the event of rolling an odd number consists of the outcomes 1, 3, 5.
In a random experiment, an event is assigned a probability.
Probability notation
Probability notation is often used to symbolize concepts in educational and technical contexts. In notation, the letter P indicates the probability of an event. The letters A and B represent individual events.
For example, if we’re dealing with two events, we can label one event A and the other event B.
- The probability of event A is written as P(A).
- The probability of event B is written as P(B).
- For any event A, 0 ≤ P(A) ≤ 1. In other words, the probability of any event A is always between 0 and 1.
- If P(A) > P(B), then event A has a higher chance of occurring than event B.
- If P(A) = P(B), then event A and event B are equally likely to occur.
Basic rules of probability
Complement rule
Complement of an event – The event not occurring (eg. the complement of rain is no rain). The two probabilities, the probability of an event happening and the probability of it not happening, must add to one.
P(A’) = 1 – P(A)
P(no rain) = 1 – P(rain)
Addition rule
Mutually exclusive events – Two events are mutually exclusive if they cannot occur at the same time. (we can’t turn left and right at the same time)
Addition rule (for mutually exclusive events):
P(A or B) = P(A) + P(B)
P(rolling a 2 or rolling a 4) = P(rolling a 2) + P(rolling a 4)
Multiplication rule
Independent events – Two events are independent if the occurrence of one event does not change the probability of the other event.
Multiplication rule (for independent events):
P(A and B) = P(A) * P(B)
P(1st toss tails and 2nd toss heads) = P(1st toss tails) * P(2nd toss heads)
These rules help us better understand the probability of multiple events.
As seen above there are two types of events: The addition rule applies to mutually exclusive events. The multiplication rule applies to independent events.
Conditional Probability
The probability of an event occurring given that another event has already occurred.
Dependent events – Two events are dependent if the occurrence of one event changes the probability of the other event.
Conditional probability P(A and B) = P(A) * P(B|A)
P(A and B) = probability of event A and event B
P(A) = probability of event A
P(B|A) = probability of event B given event A (event B depends on event A happening)
We can also represent the same equation as:
P(B|A) = P(A∩B) / P(A)
A sample (when we draw a card without replacement):
P(A) = ace on first draw = 4/52
P(B|A) = ace on second draw = 3/51
P(A and B) = ace on first draw and second draw = 4/52 * 3/51 = 1/221 =~0.5%
Note: The conditional probability formula also applies to independent events. When A and B are independent events, P(B|A) = P(B). So, the formula becomes P(A and B) = P(A) * P(B). This formula is also the multiplication rule that was introduced earlier.
Bayes’ Theorem
Bayes’ Theorem applications are found in:
- Artificial intelligence
- Medical testing
- Financial institutions (~to rate the risk of lending money to borrowers or to predict the success of an investment)
- Online retailers (~whether or not users will like certain products and services)
- Marketers (~for identifying positive or negative responses in customer feedback)
Prior probability is the probability of an event before new data is collected.
Posterior probability is the updated probability of an event based on new data.
For example, let’s say a medical condition is related to age. We can use Bayes’ theorem to more accurately determine the probability that a person has the condition based on age. The prior probability would be the probability of a person having the condition. The posterior or updated probability would be the probability of a person having the condition if they’re in a certain age group.
Bayes’ theorem is the foundation for the field of Bayesian statistics, also known as Bayesian inference, which is a powerful method for analyzing and interpreting data in modern data analytics.
P(A|B) = P(B|A) * P(A) / P(B)
P(A) = Prior probability
P(A|B) = Posterior probability
P(B|A) = Likelihood
P(B) = Evidence
Using these terms, we can restate the Bayes’ theorem as:
Posterior = Likelihood * Prior / Evidence
One way to think about Bayes’s theorem is that it lets us:
- transform a prior belief, P(A),
- into a posterior probability, P(A|B), using new data.
The new data are:
- the likelihood, P(B|A),
- and the evidence, P(B).
A sample: Weather probability calculation
- Overall chance of rain: 10 %
- All days start off cloudy: 40%
- Rainy days start off cloudy: 50%
Event A = Rain
Event B = Cloudy
P(Rain|Cloudy) = P (Cloudy|Rain) * P (Rain) / P (Cloudy)
= (0.5 * 0.1) / 0.4 = 0.125 = 12.5%
Another sample: Spam filter
- The probability of an email being spam is 20%.
- The probability that the word “money” appears in an email is 15%.
- The probability that the word “money” appears in a spam email is 40%.
Let’s calculate the probability that an email is spam given a specific word (‘money’) appears in the email.
Event A = Spam
Event B = Money
P (Spam | Money) = P(Money | Spam) * P(Spam) / P(Money)
= 0.4 * 0.2 / 0.15 = 0.53333 = 53.3 %
Bayes’ Theorem (expanded version)
When we don’t know the P(B), we can use the extended version of Bayes’ Theorem. This longer version of Bayes’ theorem is often used to evaluate tests such as:
- medical diagnostic tests
- quality control tests
- software test (such as spam filters)
When evaluating the accuracy of a test, Bayes’ Theorem can take into account the probability for testing errors, known as false positives and false negatives.
False positive – Test result that indicates something is present when it really is not.
False negative – Test result that indicates something is not present when it really is.
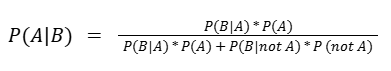
A sample: Evaluate the accuracy of a diagnostic test
- 1 % of the population has the medical condition (having an allergy)
- If a person has the condition, there’s a 95% chance that the test is positive
- If a person does NOT have the condition, there’s still a 2% chance that the test is positive (false positive)
Event A = actually having the medical condition
Event B = testing positive
P(A|B) = P(B|A) * P(A) / ( P(B|A) * P(A) + P(B|not A) * P (not A) )
= 0.95 * 0.01 / 0.95 * 0.01 + 0.02 * 0.99 = 0.324 = 32.4%
32.4 percent may seem low to us, it’s because the allergy is rare to begin with. It’s not very likely that a random person will both test positive and have the allergy.
(This above is easier to understand with a conditional probability tree diagram example.)
