Statistics is the study of the collection, analysis, and interpretation of data.
While descriptive statistics describe or summarize the main features of a dataset, inferential statistics make inferences about a dataset based on a sample of the data.
Introduction
The role of statistics in data science
As the amount of data grows, so does the need to analyze and interpret it. Data professionals use the power statistical methods to:
- identify meaningful patterns and relationships in data,
- analyze and quantify uncertainty,
- generate insights from data,
- make informed predictions about the future,
- solve complex problems.
Some statistical concepts (and real world samples):
- Probability (predict the future rate of return on an investment)
- Average (estimate the annual average sales revenue for a company)
- Margin of error (quantify the uncertainty of an employee satisfaction survey)
- Percentile (rank median home prices in different cities)
- Median
Over the basics, we can list some more complex methods too:
- Hypothesis testing
- Classification
- Regression
- Time series analysis
Main Steps of an A/B Test:
- Analyzes a small group of users (sampling)
- Decide on the sample size
- Confidence interval – a range of values that describes the uncertainty surrounding an estimate.
- (after the test is complete)
- Determine the statistical significance – the claim that the results of a test or experiment are not explainable by chance alone.
Descriptive Statistics
Descriptive statistics describe or summarize the main features of a dataset. Descriptive stats are very useful because they let us quickly understand a large amount of data.
Forms of descriptive stats:
- Visuals, like graphs and tables
- Summary stats (like mean value)
Measures of central tendency such as the mean allow us to describe the center of a data set. Measures of dispersion like standard deviation let us describe the spread of data. Measures of position such as percentiles help us determine the relative position of the values in the dataset.
Measures of central tendency
Mean – average value in a dataset.
Median – middle value in a dataset (meaning half the values in the dataset are larger than the median and half are smaller). If there are outliers, it is better to use median.
Mode – most frequently occurring value in a dataset. The mode is useful when working with categorical data because it clearly shows us which category occurs most frequently.
Measures of dispersion
Range – the difference between the largest and smallest value in a dataset.
Standard deviation – measures how spread out the values are from the mean of a dataset.
Variance – the average of the squared difference of each data point from the mean (basically it’s the square of the standard deviation).
There are different formulas to calculate the standard deviation for a population and a sample. As a reminder, data professionals typically work with sample data, and they make inferences about populations based on the sample. So, let’s review the formula for sample standard deviation:
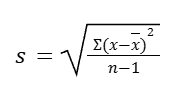
In the formula, n is the total number of data values in our sample, x is each individual data value, and x̄ (pronounced “x-bar”) is the mean of our data values.
Measures of position
Determine the position of a value in relation to other values in a dataset.
Percentiles – the value below which a percentage of data falls. Useful for comparing values. Percentiles divide our data into 100 equal parts. Percentiles give the relative position or rank of a particular value in a dataset.
Note: Percentiles and percentages are distinct concepts. For example, say we score 90/100 or 90%, on a test. This doesn’t necessarily mean our score of 90% is in the 90th percentile. Percentile depends on the relative performance of all test takers. If half of all test takers score above 90%, then a score of 90% will be in the 50th percentile.
Quartiles – divides the values in a dataset into four equal parts. Useful to get a general understanding of the relative position of values. A quartile divides the values in a dataset into four equal parts.
Q1: 25th percentile or the median of the lower half of the dataset
Q2: 50th percentile or the median of the entire dataset
Q3: 75th percentile or the median of the upper half of the dataset
Interquartile range – the distance between the Q1 and Q3 or the middle 50% of the data. Useful for determining the relative position of our data values. For instance, data values outside the interval Q1 – (1.5 * IQR) and Q3 + (1.5 * IQR) are often considered outliers.
Five number summary – includes:
The minimum
The first quartile (Q1)
The median, or second quartile (Q2)
The third quartile (Q3)
The maximum
Useful because it gives us an overall idea of the distribution of our data from the extreme values to the center. It can be visualized with a box plot.
Inferential Statistics
Inferential statistics make inferences about a dataset based on a sample of the data.
Population – every possible element that we are interested in measuring (can be people, objects, or even events).
Sample – a subset of a population (should be representative of the population).
Parameter – a characteristic of a population.
Statistics – a characteristic of a sample.
Forms of inferential stats:
- Sampling
- Confidence intervals
- Hypothesis testing
